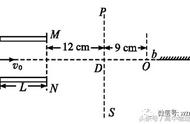
计算回路形状变化导致的磁通量变化
接下来是磁通量变化率右侧的第二项。如上图,考察一小段(有向)导线d=d,其运动速度记为,不难看出在经过一小段时间d后,该小段导线的运动使得回路增加了一个(有向)面积元(d)×d,进而导致增加的磁通量为()∙[(d)×d]。通过三矢量混合积的公式可以将其整理为-dd∙(×)。将整个回路的每一小段导线的贡献都加起来再除以d,就得到磁通量变化率右侧第二项为

将两项合并,得到:

这样一来,我们发现右侧被积函数括号内正是单位电荷受到的非静电力,根据电动势的定义立刻得到:

这正是“通量法则”。