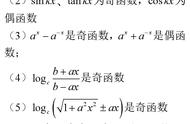画出图像,可以看到这个函数的图像是关于原点对称的:

有了定义,也知道了函数在图像上的表现,那么判断一个函数是奇函数还是偶函数就简单了,遵循以下步骤即可:
1、确认这个函数的定义域是否关于原点对称,如果不对称,那你就别费功夫了,它就不可能是奇函数或者偶函数,只能是非奇非偶函数。
也就是说,函数不一定非要是奇函数或者偶函数中的一种,也可以啥都不是。
2、在确保定义域对称的情况下,找出互为相反数的两个自变量,观察它们对应的函数值f(x)和f(-x),如果相等,就是偶函数;如果相反就是奇函数。
既不相等也不相反,非奇非偶函数。
实际的练习过程中,这种给出自变量,让你直接判断的机会很少,因为大多数习题都会故意出的比较复杂,没有办法直接找到f(x)和f(-x),你只能另寻其它的渠道,比如采用二者相加减的形式,相减为0,为偶函数;相加为0,奇函数,
这才是使用判断函数奇偶性的日常操作。
3、对于分段函数,必须保证在定义域的任何一个分段内,都符合奇函数或者偶函数的定义,只要有一个分段不符合定义,那这个函数就不能判定它的奇偶性。
4、还有一种常考到的抽象函数,也就是没有表达式的那种,这种函数从头到尾就没有固定的办法去判断它的奇偶性。不过,很多时候,题目会给出相关函数之间的关系等式,通过这种等式,我们可以创造出f(x)和f(-x),然后判断它们之间的关系就可以了。
举个例子:

对于这种题目,你可以大胆的想办法创造出f(x)和f(-x),反正定义域是实数集,你完全可以任意地往给出的关系式代入取值,只要创造出f(x)和f(-x),,一切就简单了。
5、注意!!!这一点非常重要,是常考内容,必须切实掌握:
如果知道了函数奇偶性,可以根据复合函数的奇偶性,演化出自变量函数的周期性或者对称性,举个例子:
如果给出符合函数f(x 1)为偶函数,那么根据偶函数的定义,
我们可以写出:f(x 1)=f(-x 1)。
这时候我们发现,如果我们在坐标轴上找到1这个点,从这个点开始,函数往左移动一个x,它对应的函数值f(-x 1)和往右移动一个x的函数值f(x 1)是相等的,那么现在我们就可以得出明确的结论,那就是函数f(x)关于x=1轴对称。
6、如果给出的题目是一个非奇非偶函数函数,那么我们是否可以把这个非奇非偶函数拆开呢?
比如说这样一个函数,它本身是一个奇函数和一个偶函数相加得来的:
如:F(x)=f(x) g(x)
如果我们能知道f(x)是偶函数,g(x)是奇函数,我们就可以很轻松的把这个函数拆分成两部分:
此时

这样和原式联立起来,即可将偶函数、奇函数拆出来。
上面的例子如果觉得抽象的话,我们还可以用具体的例子来尝试下:
比如我们给出这样一个非奇非偶函数: