圆球的表面积公式是怎么推导的,圆球表面积怎么计算公式

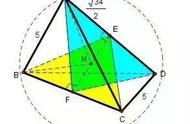
各位同学，你们知道球体的表面积和体积公式吗？也许有的同学多学了一些知识可以直接说出来。但是如果让各位同学写出推导公式，又有多少人能写出呢？球体的一些通用公式大都是用微积分来推导的，今天我们就来讲一个不用微积分就能“算球”的好方法。

首先，抛弃了微积分这一曲线计算利器，我们的替代工具是：一点点相似三角形知识，一点点空间想象力，再加上中国古代数学家智慧的结晶——祖暅原理。

众所周知，球的表面积公式是 4πr2，正好是同半径圆形面积的 4 倍，这不禁让人浮想联翩，为什么正好是 4 倍呢？难道圆形面积和球体面积之间有什么不可告人的秘密？顺着这个思路下去你可能会觉得完全无从下手，感到弱小，可怜，又无助。

这也正是我初期经历的心路历程，直到我发现了另一个秘密：4πr2 正好是这个球外接圆柱的外围面积。

Credit: 3blue1brown

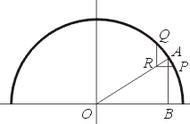
想象一下，如果把球表面划分小块，沿水平向四周投影，按理来说，这样投出的小块就可以正好铺满外面这个”圆筒”。因为圆筒的面积是圆周长乘上筒高：2πr*2r = 4πr2，和里面这颗球的表面积不谋而合！

就像下图右上角示意的那样，球上的小块被投影到圆筒上会变形，它们的宽度可能增大，而高度会相应变小。

Credit: 3blue1brown

小块可以从平视和俯视两个方向来观察。那我们就来看看，投影过程中，我们的小块到底经历了什么不为人知的变化。