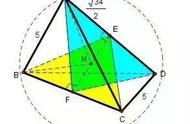
b. 四棱锥每一个横截面都是边长为 h 的正方形(斜视图)
这下好了,仅仅是做了个除法,问题似乎已经简单多了!
但你可能还是会问,四棱锥的体积又要怎么计算呢?别着急,我们先好好观察一下这个四棱锥。它的顶点在中心上方,感觉还是不够友好,怎么能再变换一下形状呢,没错,是时候祭出祖暅原理了。

把顶点移到一个角上,新的四棱锥有三条互相垂直的边,并且体积不变
到了这里,问题基本上已经解决了。什么,你还没看出来?调动你的空间想象力,调整一下角度,把这样的四棱锥放在正方体里似乎正合适,你能看出可以同时放进几个吗?

为了让你们相信是 3 个而精心制作的 gif 动图
是 3 个!万事大吉~
正方体的体积显然是 r3,这样一来,四棱锥体积就是 r3/3。接着,对应圆锥的体积只需要乘上 π,V圆锥 = r3/3*π。最后半球的体积 V半球 = V圆柱 - V圆锥 = πr3-πr3/3 = 2/3 (πr3),所以 V球 =4/3 (πr3),是不是和书上写的公式一模一样呢!
成功算球!完结撒花~
作为一期数学类的硬核推送,小编想说的是,很多时候只要切换一下思路,尝试别的工具,就可能开辟出新的道路。
所谓的数学之光,我想也就是在这里。
- 编辑:Chaos
- 审核:Tong
- 来源:中科院物理所