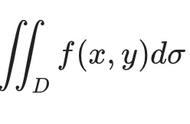1. 向量1. 平面向量/点积
2. 向量值函数
3. 笛卡尔坐标/点积/叉积
4. 空间中的直线和平面
5. 柱面和二次曲面
6. 向量值函数和空间曲线
7. 弧长和单位切向量
8. TNB标架;加速度的切向分量和法向分量
9. 多元函数
10. 高维函数的极限和连续
11. 偏导数
12. 方向导数, 梯度向量和切平面
13. 线性化和全微分
14. 极值和鞍点
15. Lagrange 乘子
16. 两个变量的 Taylor 公式
17. 二重积分
18. 极坐标下的二重积分
19. 直角坐标系下的三重积分
20. 线积分
21. 向量场
22. 第二类线积分, 环量和流量
23. 与路径无关, 势函数与保守场
24. 平面的格林(Green)定理
25. 曲面面积和曲面积分
26. 参数化曲面
27. Stokes 定理
28. 散度定
▌平面向量
测量某些事物的大小, 如质量, 长度和时间, 只需要一个数和一个测量单位. 相关实数为标量.
向量(vector, 或称矢量)是指一个同时具有大小和方向的几何对象, 可以用来描述力, 位移或速度.

只要向量的大小和方向相同, 即视为相等的向量. 另外如果向量 v 的起点在原点, 则称之为是 v 的标准位置. 观察如下图所示在二维平面(Two-dimensional)下, 当移动一个向量, 所留下轨迹上都视为相同的向量:

向量的分量形式:如果平面上的一个向量 v 等于起点在原点 (0,0) 终点在 (v1, v2) 的向量, 则 v 的分量形式是 v=(v1,v2)

向量 v 的长度表示成 |v| 或 ||v||.
任何长度为 1 的向量 v 为单位向量. 如果 v=(v1,v2)与正 x 轴成角 θ , 则 v=(cosθ, sinθ) . 当 θ 从 0 到 2π 时, 单位向量取遍所有可能方向, 则绘制出单位圆.