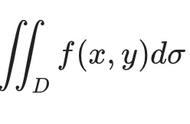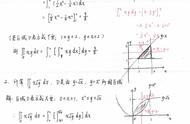二重积分的斯托克斯公式是数学分析中的重要公式之一,它描述了二重积分与被积函数在积分区域上的积分之间的关系。该公式在积分学中有广泛的应用,例如在计算面积、体积和表面积等方面。
首先,我们需要了解斯托克斯公式的定义。斯托克斯公式表述为:如果f(x, y)是定义在有界闭区域D上的连续函数,且z=f(x, y)表示的曲面在D上下的面积等于该曲面围成的立体表面积的负值,那么f(x, y)在D上的二重积分等于f(x, y)围成的立体表面积的负值。
为了更好地理解斯托克斯公式,我们可以从几何和代数两个角度来解释它。从几何角度来看,斯托克斯公式告诉我们一个曲面的面积可以通过其在某个平面上的投影的面积和该投影面积上每一点的法向量与z轴之间的角度的正弦值的乘积来计算。从代数角度来看,斯托克斯公式可以看作是计算二重积分的一种简化方法,它通过将被积函数表示为面积分的形式,使得计算更加简便。
接下来,我们可以通过一些具体的例子来进一步理解斯托克斯公式的应用。例如,如果我们有一个曲面z=f(x, y),我们可以通过斯托克斯公式来计算该曲面的面积。首先,我们需要确定该曲面的投影面积,然后计算每一点的法向量与z轴之间的角度的正弦值,最后将这些值与投影面积相乘并求和即可得到曲面的面积。
此外,斯托克斯公式在计算体积和表面积等方面也有广泛的应用。例如,如果我们有一个旋转曲面,我们可以通过斯托克斯公式来计算它的表面积。首先,我们需要确定该旋转曲面的半径和高度,然后计算其母线与z轴之间的角度的正弦值,最后将这些值与旋转曲面的表面积相乘即可得到结果。
在实际应用中,我们需要注意一些问题。首先,斯托克斯公式只适用于有界闭区域上的连续函数,对于不满足这些条件的函数可能需要其他的方法来计算二重积分。其次,在实际计算中我们需要考虑计算的精度和误差控制,以避免出现计算错误或精度损失等问题。
综上所述,二重积分的斯托克斯公式是数学分析中的重要公式之一,它描述了二重积分与被积函数在积分区域上的积分之间的关系。该公式在积分学中有广泛的应用,例如在计算面积、体积和表面积等方面。通过几何和代数两个角度的理解,以及具体例子的计算和分析,我们可以更好地掌握斯托克斯公式的应用方法和技巧。在实际应用中,我们需要注意适用条件和误差控制等问题,以确保计算的准确性和可靠性。