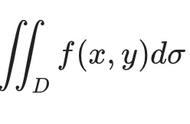▌把一个向量写成正交向量的和
在研究一个质点沿平面上(或空间中)的一个路径的运动时, 加速度向量就可以写成它的切向分量和法向分量之和.

▌平面曲线
当一个质点在时间区间 I 在平面内运动时, 可以把质点的坐标看做在 I 上的函数

点(x,y) = (f(t), g(t)) 形成平面上的曲线, 称它为质点的路径. 从原点到质点在时刻 t 的位置 P(f(t),g(t)) 的向量

是质点的位置向量, 函数 f 和 g 是位置向量的分量函数(分量). 质点的路径是在时间区间 I 由 r 绘制的曲线. 观察下面的向量函数