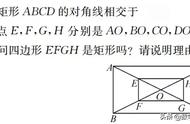
矩形。
今天我们来学习矩形,它是一种特殊的平行四边形。有同学这个矩不会读的,要学一下矩形。那什么是矩形?
·首先来看这个,这是一个平行四边形,现在保持它的四边长度不变,这个是关键。
·然后这样水平移动CD,移动的过程中四个角发生变化,四条边不变。
·当这个角A是怎样的角的时候,它才能变成我们熟悉的一个小学学过的长方形?我们能够看到,当这个角A变成一个直角的时候,它就能变成长方形,也就是我们初二说的矩形。

·那么矩形的定义,它是由平行四边形而特殊化,需要有一个角是直角,有一个角是直角的平行四边形是矩形,这就是矩形的定义了。
·那现在我们来看矩形,它具有怎样的特性?首先它是平行四边形,它具有平行四边形的一切特征,包括两组对边分别平行,两组对边分别相等,两组对角分别相等,对角线互相平分。

·刚才我们说两组对角分别相等,角A是直角,那么角C也是直角,还有两组对边分别平行。
·我们来看两直线平行,同旁内角互补,那么角D也是90度,同旁内角互补,角B也是90度。
所以它矩形,它具有平行四边形不具有的重要特征,是四个角都是直角。
·还有一个要素是对角线,矩形的对角线有怎样特殊的性质?我们先来猜一下,把对角线连起来,大概猜一下相等,是相等的,矩形的对角线相等。

·现在我们来证明,为什么矩形的对角线相等,也就是需要证明AC等于BD,证明对角线相等。AC能BD需要用什么武器?用三角形全等,三角形ACB ACB,BDA。

·我们来看需要怎样的条件?首先,AB等于BA,这是公共边,还有CB等于DA,这是对边相等。
·矩形的4个角都是直角,那么这里面含有角ABC,等于ABC等于角BAD,所以我们就可以通过边角边能证明这两个三角形全等,同时就证明它们的对角线相等。
,