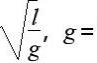在高中物理阶段,单摆是一种非常重要的简谐运动模型,本节就对单摆及其相关知识进行介绍。
我们首先来认识下单摆。
并不是所有的悬挂起来的摆动都是单摆,要想成为我们要研究的理想物理模型的单摆还需要满足以下几个条件:
1、悬挂小球或者物体的细线的长度不可改变;
2、细线的质量与悬挂的小球或者物体相比,质量可以忽略;
3、悬挂小球的直径或者物体的尺寸相对于细线的长度来说也可以忽略;
4、与悬挂小球的所受到的重力及绳的拉力相比,空气对小球以及绳的阻力可以忽略;这也是为什么我们要选择质量大体积小的球,以及比较细的绳的原因;
满足以上几个条件,才能成为我们要研究的理想的物理模型:单摆。
那么,我们接下来就要研究了,在什么样的条件下,单摆的运动才是简谐运动呢?
根据前面介绍的简谐运动的知识,我们可以从两个方面来探究这一问题:
其一是,我们可以从小球的受力情况来分析,我们来看下其受到的力是不是满足回复力的特性要求?即小球所受到的回复力是不是与其位移成正比,方向与位移相反。如果能满足以上要求,那么,单摆所做的运动就是简谐运动。
其二是,我们可以从小球的运动的位移与时间的函数关系来看,看其是不是满足正弦函数的关系,如果满足,那么,单摆所做的运动就是简谐运动。
我们来分析下,在θ角很小的情况下,摆动的小球所受到的重力沿弧线方向的分力提供小球摆动的回复力。
即:F=mgsinθ
根据数学知识我们知道,在θ角很小的情况下,其弧度制近似等于其sinθ值。
所以,sinθ近似等于x/l,其其中x为小球摆动位移。
在θ角很小的情况下,我们可以认为弧线为直线,我们可以认为回复力的方向始终与x的方向相反。
从以上分析可以知道,单摆的回复力可以表示为:
F=-mg/l*x
其中对于确定的单摆来说,mg/l为常数,我们设为k
最后单摆的回复力就可以表示为:
F=-kx
所以,由以上可见,单摆在摆动角度很小的情况下是在做简谐运动。
最后我们来介绍下,单摆在做简谐运动时的周期。
实验表明,单摆的周期和摆长的长度有关,摆场越长,单摆的周期越大,单摆的周期与摆球的质量和单摆的振幅都无关。
为了找出单摆的周期与单摆的摆长之间的定量关系,荷兰物理学家惠更斯进行了大量的实验和理论研究,最终,惠更斯得出,单摆的周期与摆长的二次方根成正比,与重力加速度的二次方跟成反比,而与摆球的质量以及单摆的振幅都没关系。
最终,惠更斯给出了单摆在做简谐运动时的周期公式:
单摆的周期公式的发现为后来人们利用单摆的简谐运动来定量计时提供了可能。
80后的同学应该对摆动座钟有印象,摆钟就是利用摆动重锤作为振动系统的计时仪器,起源于意大利人伽利略对钟摆等时性的发现,其后荷兰人惠更斯于1656年正式制造发明了摆钟。它就是利用了单摆摆动的等时性制作而成的。
以上就是关于单摆的相关知识的介绍,供大家学习和参考。
,