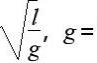单摆是高中物理选修3-4中第一章机械振动第二节内容。我们知道,当摆角小于时,单摆的振动是简谐运动。根据实验探究发现单摆做简谐运动的周期与振幅、摆球的质量无关,只与摆长和重力加速度有关,单摆周期公式为。
在解决实际振动问题中,常常涉及类单摆振动问题,以及单摆在不同环境中振动问题。对这些问题的解决就需要弄清楚两个问题,第一个问题是决定单摆振动快慢的实质是什么?第二个问题是单摆的周期公式是在什么条件下探究得到的?
如图1所示是单摆的理想模型。

图1
单摆在振动过程中同时又在做圆弧运动,摆球受重力和绳子的拉力。绳子的拉力和重力沿绳方向的分力的合力提供摆球做圆弧运动的向心力,其只改变摆球运动速度的方向。而重力沿圆弧切线方向的分力提供摆球做简谐运动的回复力,其只改变摆球运动速度大小,也就决定了摆球振动快慢。因此,回复力是改变摆球振动快慢的原因,是判断单摆振动周期是否变化的依据。
在实验室(惯性参考系)中,摆球只受重力和绳子的拉力情景下,通过实验探究,得到单摆做简谐运动的周期公式。如果单摆所处的环境变了、摆球所受力变了,其振动的周期将会怎样变化呢?我们可通过与单摆的理想模型对比分析,找到正确的结果。
下面举几个典型的情景分析。
情景1:类单摆问题。
如图2所示,小球在一圆弧曲面上振动。

图2
小球振动过程中,其受重力和圆弧面的支持力,而且该支持力方向始终指向圆心。与单摆的理想模型对比,圆弧面对小球的支持力相当于单摆中绳子对摆球的拉力,小球振动的回复力也是重力沿圆弧切线方向的分力提供,因此其振动周期为。
例1:如图3所示,光滑轨道的半径为2 m,C点为圆心正下方的点,A、B两点与C点相距分别为6 cm与2 cm,a、b两小球分别从A、B两点由静止同时放开,则两小球相碰的位置是( )

图3
A.C点
B. C点右侧
C.C点左侧
D.不能确定
答案: A
解析: 由于光滑轨道的半径远远大于运动的弧长,小球都做简谐运动,类似于单摆.因此周期只与半径有关,与运动的弧长无关,两球都经四分之一周期同时到达C点相碰,故选项A正确.
情景2:单摆在磁场中的振动。
如图4所示,一摆球带正电的单摆在垂直于匀强磁场的竖直平面内振动。