问题,已知x<2, 求f(x)的最小值,

解法1:因为2-x>0,利用算数平均大于几何平均数的不等式有,

因此f(x)最小值是2.
取得最小值的时候有:

解这个方程为x-2=1, 或x-2=-1, 但x<2, 所以x=1时有最小值。

解法2:
因为原有的式子可以化为

而右边的第一项在x<2的时候,总是大于等于零,只有分子在x=1的时候才会有最小值为零,所以整个式子的最小值为2.
,问题,已知x<2, 求f(x)的最小值,

解法1:因为2-x>0,利用算数平均大于几何平均数的不等式有,

因此f(x)最小值是2.
取得最小值的时候有:

解这个方程为x-2=1, 或x-2=-1, 但x<2, 所以x=1时有最小值。

解法2:
因为原有的式子可以化为

而右边的第一项在x<2的时候,总是大于等于零,只有分子在x=1的时候才会有最小值为零,所以整个式子的最小值为2.
,


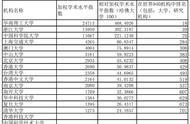





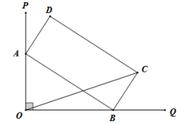





Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.