【要点梳理】
要点一:平方根和立方根

要点二:实数
有理数和无理数统称为实数.
1.实数的分类
按定义分:
按与0的大小关系分:
2.实数与数轴上的点一 一对应.
数轴上的任何一个点都对应一个实数,反之任何一个实数都能在数轴上找到一个点与之对应.
3.实数的三个非负性及性质:
在实数范围内,正数和零统称为非负数。我们已经学习过的非负数有如下三种形式:
(1)任何一个实数的绝对值是非负数,即|a|≥0;
(2)任何一个实数的平方是非负数,即a2≥0;
(3)任何非负数的算术平方根是非负数。
非负数具有以下性质:
(1)非负数有最小值零;
(2)有限个非负数之和仍是非负数;
(3)几个非负数之和等于0,则每个非负数都等于0.
4.实数的运算:
数a的相反数是-a;一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数;0的绝对值是0.
有理数的运算法则和运算律在实数范围内仍然成立.实数混合运算的运算顺序:先乘方、开方、再乘除,最后算加减.同级运算按从左到右顺序进行,有括号先算括号里.
5.实数的大小的比较:
有理数大小的比较法则在实数范围内仍然成立.
法则1. 实数和数轴上的点一一对应,在数轴上表示的两个数,右边的数总比左边的数大;
法则2.正数大于0,0大于负数,正数大于一切负数,两个负数比较,绝对值大的反而小;
法则3. 两个数比较大小常见的方法有:求差法,求商法,倒数法,估算法,平方法.
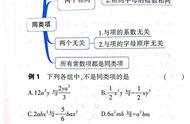
【习题讲练】


第四章复习
【知识网络】