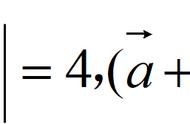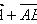【单位向量】:模为1的向量就是单位向量。
【向量的基(也称为基底)】:给定一个向量空间 V。 V的一组基B,是指V里面的可线性生成V的一个线性无关子集。B的元素称为基向量。
1.2 常见运算
向量常见的运算有:加法,减法,标量乘向量以及向量之间的乘法(叉乘、点乘)。
在机器学习中,我们需要重点看加法,标量乘向量和点乘。
设:存在两个n维度向量a = (a1, a2, …, an) 和 b = (b1, b2, …, bn)
1.2.1 向量加法
a b = (a1 b1, a2 b2, …, an bn)
1.2.2 向量乘以标量
设标量为k, 则 ka = (ka1, ka2, …, kan)
1.2.3 向量点乘

1.3 向量性质
1.3.1 线性相关(linearly dependent)
假设V是在域K上的向量空间。V中的一组(m个)元素中,若有向量可用有限个其他向量的线性组合所表示,则称为线性相关,反之称为线性无关。
换言之,如果v1, v2, ..., vn 是V的向量,如果从域K 中有非全零的元素a1, a2, ..., an,适合 a1v1 a2v2 ... anvn = 0, 则称它们为线性相关。
如果K中不存在这样的元素,那么v1, v2, ..., vn是线性无关或线性独立。
1.3.2 线性相关的几何意义
说向量组v1, v2, ... vm 线性相关,则:
当m = 1时,若v1 = 0, 则只含有v1一个元素的向量组线性相关,否则,线性无关。
当m = 2时,如果 a1v1 a2v2 = 0,则v1和v2线性相关,也就是说v1和v2的分量对应成比例,在几何意义上,v1和v2共线。否则,二者线性无关。
当m =3时, v1,v2,v3线性相关的几何意义是三者共面。
1.3.3 正交
若内积空间中两向量的内积为0,则称它们是正交的。正交是垂直这一直观概念的推广。
1.3.4 正交 vs 线性无关
正交的向量一定线性无关,线性无关的向量不一定正交。
2. 线性变换与线性函数2.1 线性变换
在两个向量空间之间的一种保持向量加法和标量乘法的特殊映射,称为线性变换(或线性映射)。
2.2 线性函数
设 V 和 W 是在相同域 K 上的向量空间。法则 f : V → W 被称为是线性映射,如果对于 V 中任何两个向量 x 和 y 与 K 中任何标量 a,满足下列两个条件:
(1) 可加性: f(x y) = f(x) f(y) (2) 齐次性: f(ax) = af(x)
即其维持向量加法与标量乘法。
上述等价于要求对于任何向量 x1, ..., xm 和标量 a1, ..., am,下面方程成立:

当上述的法则 f : V → W为函数时,就是线性函数。
比较直观的理解就是大部分一次函数,例如二维空间中的f(x)=ax b,其中a,b为常数。
3. 矩阵3.1 m x n 矩阵
3.1.1 定义
将一些元素排列成若干行,每行放上相同数量的元素,就是一个矩阵。
一个m×n的矩阵是一个由m行n列元素排列成的矩形阵列,矩阵里的元素可以是数字、符号或数学式。
3.1.2 矩阵的基本运算
最基本运算包括矩阵加(减)法,数乘和转置运算。
【1】矩阵加法:m×n矩阵A和B的和(差):A±B为一个m×n矩阵,其中每个元素是A和B相应元素的和(差): (A ± B)i,j = Ai,j ± Bi,j,其中1 ≤ i ≤ m , 1 ≤ j ≤ n.
【2】矩阵数乘:标量c与矩阵A的数乘:cA的每个元素是A的相应元素与c的乘积,(cA)i,j = cAi,j
【3】矩阵转置:m×n矩阵A的转置是一个n×m的矩阵,记为AT(或A'),其中的第i个行向量是原矩阵A的第i个列向量;或者说,转置矩阵AT第i行第j列的元素是原矩阵A第j行第i列的元素, (AT)i,j = Aj,i
【4】矩阵的乘法:两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积AB是一个m×p矩阵,它的一个元素

其中1 ≤ i ≤ m, 1 ≤ j ≤ p
3.1.3 矩阵运算的规律
[1] 矩阵的加法运算满足交换律:
A B = B A。
[2] 矩阵的转置和数乘运算满足分配律:
(A B)T = AT BT c(A B) = cA cB
并满足类似于结合律的规律: c(AT) = (cA)T.
[3] 矩阵的乘法满足结合律和对矩阵加法的分配律(左分配律和右分配律):
• 结合律:(AB)C = A(BC), • 左分配律:(A B)C = AC BC, • 右分配律:C(A B) = CA CB.
[4] 矩阵的乘法与数乘运算之间也满足类似结合律的规律:
c(AB) = (cA)B = A(cB)
[5] 矩阵的乘法与转置之间则满足倒置的分配律:
(AB)T = BTAT
[6] 矩阵乘法*不*满足交换律。
一般来说,矩阵A及B的乘积AB存在,但BA不一定存在,即使存在,大多数时候AB ≠ BA。
3.1.4 矩阵与线性变换的关系
矩阵是线性变换的便利表达法。
以R^n表示所有长度为n的行向量的集合。每个m×n的矩阵A都代表了一个从R^n射到R^m的线性变换。
也就是说,对每个线性变换f: R^n -> R^m,都存在唯一m×n矩阵A使得对所有R^n中的元素x,f(x) = Ax。
3.1.5 相关基本概念
【矩阵的秩】: 用初等行变换将矩阵A化为阶梯形矩阵, 则矩阵中非零行的个数就定义为这个矩阵的秩。
【列秩】:一个矩阵A的列秩是A的线性独立的纵列的最大数目。
【行秩】:一个矩阵A的行秩是A的线性独立的横行的最大数目。
行秩和列秩的关系:矩阵的列秩和行秩总是相等的。因此它们可以简单地称作矩阵A的秩。通常表示为r(A),rk(A)或rank A。
【满秩矩阵(non-singular matrix)】:若矩阵秩等于行数,称为行满秩;若矩阵秩等于列数,称为列满秩。既是行满秩又是列满秩则为n阶矩阵即n阶方阵。
【子式】:设A为一个 m×n 的矩阵,k为一个介于1和m之间的整数,并且k≤n。A的一个k阶子式是在A中选取k行k列之后所产生的k2个交点组成的方块矩阵的行列式。
【余子式】:A的一个k阶余子式是A去掉了k行与k列之后得到的(m-k)×(n-k)矩阵的行列式。
NOTE: 在m=/=n的情况下,这样的行列式如何计算是没有定义的,仅仅在概念上存在。
【零矩阵】:即所有元素皆为0的矩阵。
NOTE:对称矩阵,对角矩阵,矩阵的对角化等都有针对mxn矩阵的一般定义,但是在应用的层面,我们不必进行这些一般性的讨论,而只需要关注其针对nxn阶方阵的情形即可,因此,大多数情况下,对于矩阵的性质和运算,我们集中关注方阵这一特例。
3.2 n x n方阵
方阵具备一些一般m x n矩阵(m =/= n) 所不具备的特征和属性,使得它们特别有用。而一些运算,如对角化等在方阵中比一般矩阵中多见而且更容易,因此,许多问题我们集中在方阵里讨论。
3.2.1 基本概念
【方阵】:在所有矩阵中,行和列相等的那类称为方阵。
【行列式】:将一个nxn的方阵A映射到一个标量,记作|A|或det(A)。虽然记作|A|,但其实一个矩阵的行列式有可能是负数,这里要注意和绝对值区别。
• 1阶矩阵的行列式:就是它本身。
• 2阶矩阵的行列式: