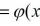函数(function)是我们初中就开始接触的一个数学概念,也是高中阶段最核心的数学概念之一,我们通常用f(x)来表示一个函数。上了大学之后,我们会更加深入地研究函数的连续性,可微性,可导性等问题。但是对于绝大多数的同学,平时所接触的函数都只是所谓的初等函数。初等函数,指的是由5大类基本初等函数:
幂函数(power function),指数函数(exponential function),对数函数(logarithmic function),三角函数(trigonometric function)和反三角函数(inverse-trigonometric function)
经过有限次加减乘除与复合所得到的函数。比如我随手写一个函数:

它可就可以看成是一个三角函数与幂函数做复合,再和指数函数做除法得到的。
你可以搜罗一下你所见到的函数,基本上都是初等函数,那么这个“初等”又是怎么回事呢?难道还有“高等”的函数吗?
的确如此,初等函数都具有一些良好的性质,比如,所有初等函数在其定义域上都是连续的,并且是几乎处处可导的,即使有一些不可导点,那这些不可导点也是有限的、孤立的。也就是说,初等函数的图像都是我们可以想象出来的,就是一段儿除了个别点之外,其余都是连续的、光滑的曲线。比如我刚才随手写的函数,它的图像就是如下的样子:

那么是否会有一些函数,它有无穷多个不可导点,甚至每一点都不可导,更有甚者,图像我们连画都画不出来?这样的函数是有的,而它显然不是我们熟悉的初等函数,因为其性质太过诡异,我们称其为“病态函数”。最简单的一类病态函数就是大名鼎鼎的狄利克雷函数。在介绍它之前,我们先来介绍一下他的发明人——德国大数学家狄利克雷(Dirichlet)。

狄利克雷(1805-1859)
狄利克雷出生于1805年,他可谓是师出名门,曾经是“数学王子”高斯(Gauss,1777-1855)的学生,同时也参加过另一位法国大数学家傅里叶(Fourier,1768-1830)领导的小组活动。他于1829年到柏林大学任教,1831年被选为普鲁士科学院院士,并于1855年接替高斯成为哥廷根大学的教授,同年被选为英国皇家学会会员。
狄利克雷在数论、分析学和数学物理等多方领域做出了杰出贡献,是19世纪上半叶非常重要的一位数学家,同时也为19世纪下半叶哥廷根大学成长为世界数学中心奠定了基础。