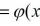可以看出这样构造出来的函数,同样具有上述三个诡异的性质。同时我们还可以对它进行改造,构造出一些更为诡异的函数,例如只在一点处连续的函数,只在一点处可导的函数等等。
上面狄利克雷函数的表达式是利用分段函数写出的,那么它有没有单个的表达式呢?数学家们发现狄利克雷函数可以利用下面这个式子来表示

小伙伴们可以思考一下,为什么它就表示狄利克雷函数。
发展狄利克雷函数的发现在20世纪有了更为重大的意义。20世纪初,法国数学家勒贝格(Lebesgue,1875-1941)通过对传统积分理论的研究,提出了一种新的定积分理论——勒贝格积分。他发现,勒贝格积分是比传统的定积分更为进步的积分,它囊括了更多的函数形式,而狄利克雷函数就是一个最典型的在传统意义下不可积,但却是勒贝格可积的函数。用更专业的语言来讲,勒贝格积分是传统积分理论的完备化,它使得人们对函数与积分的认识更上一层楼,而勒贝格积分也取代了传统的定积分理论,成为当代数学研究里面通用的积分理论。而如果想要学习勒贝格积分,就需要进一步学习测度论,这将又是一个很漫长的过程。

最后,就拿勒贝格大神的照片来镇楼吧!相信每个学习过实变函数的人看到这张照片的人都会瑟瑟发抖。
,参考文献
[1] 《高等数学》,第七版,同济大学数学系,北京,高等教育出版社
[2] 《数学分析(下册)》,第三版,华东师范大学数学系,北京,高等教育出版社
[3] Calculus, early transcendentals, 7ed, James Stewart, Brook/COLE