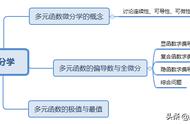
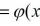十九世纪数学圣地——哥廷根大学
长久以来,人们只是把函数理解为两个变量之间的变化关系,并且通常用一个表达式来表示。1837年,狄利克雷突破了这个框架,认为函数就是集合中两个元素的对应关系,而不必非得有一个表达式,于是提出了函数就是x与y之间的一种对应关系的现代观点。我们现在教科书上的关于函数的定义,基本上就是沿袭了这种观点。

函数概念示意图
为了说明这一观点,狄利克雷就构造了一个人们以前从来没有见过的函数,就是我们现在被称之为狄利克雷函数的函数,它的函数表达式如下:

这个函数的图像让人想想就头皮发麻:在实数轴上有无数多个密密麻麻的有理数,同时还有无数多个密密麻麻的无理数。因此它的图像也是如此的诡异:在y=1的地方密密麻麻分布着无数个点,但是因为有无理数的存在,所以这些点彼此又存在无数多的空隙,不能连成一条连续的直线,同样道理,在x轴上也是如此!这样的图像我们想试用笔画出来是万万不可能的。
这里需要补充一句,有很多人说狄利克雷函数是不存在图像的,这种说法是错误的。它不是不存在图像,而是图像我们无法用笔画出。事实上,任何函数都是有图像的,对于给定的函数f(x),我们把集合
{ (x,f(x)) | x在定义域内}
称为这个函数的图像。
狄利克雷函数彻底颠覆了人们对函数的传统认识。通常人们想象出来的函数就是一段或者几段光滑的曲线,它或许有不连续点或不可导点,但都是有限多个、分散开的,但是狄雷克雷函数的图像,人们连画都无法画出来,甚至它在连续性与可导性上更加突破了人们的想象。我们就来看一下狄利克雷函数它具有哪些诡异的性质。

意思是所有的点都是间断点。我们在高等数学里面学过,函数f(x)在x=a处连续的定义是函数在该点的极限值等于该点的函数值,即它要满足