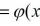不满足的话,则是不连续的。我们就拿这个定义来检验一下狄利克雷函数。当a无论取何值时,在a的任意一个小的邻域内,都有无数多个有理点和无数多个无理点,有理点处函数值为1,无理点处函数值为0,因此在a的左边和右边函数都是无穷震荡的,所以x趋近a是f(x)的极限不存在,也就更无法等于f(a)了,因此是不连续的。因为a是任意取的一个值,所以狄利克雷函数在任意一点都是不连续的。

我们高中时都学过,可导一定连续,连续不一定可导,并且不连续一定不可导,狄利克雷函数在任意一点都不连续,因此它在任意一点都不可导。
这里顺便提一下,狄利克雷函数处处不可导,是因为处处不连续。不连续导致不可导,这没什么大不了的,但在1872年,被誉为“近代分析之父”的德国数学家魏尔斯特拉斯(Weierstrass,1815-1897)构造出了一个处处连续但无处可导的函数,又进一步颠覆了人们对导数概念的理解,这是后话。

我们在高等数学中学过,一个函数f(x)在闭区间[a,b]上的定积分,它的定义就是如下的极限:

右边这个极限如果存在,则称f(x)在[a,b]上是可积的,极限如果不存在则称为不可积。
事实上,想构造出一个不可积的函数非常地困难。回想一下你在高等数学里面接触过的所有有界函数,其实都是在闭区间上可积的。而不可积的函数则只能从“病态函数”里面寻找,狄利克雷函数就是其中一个最典型的例子。