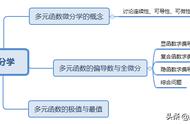
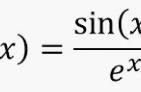狄利克雷函数:是一个定义在实数范围内,值域不连续的函数。狄利克雷函数的图像以Y轴为对称轴,是一个偶函数,它处处不连续,处处极限不存在,不可黎曼积分。这是一个处处不连续的可测函数。
实数域上的狄利克雷(Dirichlet)函数表示为:

其中:k,j 为整数。
也可以简单的表示为分段函数的形式,如下:

狄利克雷函数的性质:
- 1,定义域为整个实数域R,值域为{0, 1},函数为偶函数
- 2,无法画出函数周期,但是它的函数图像客观存在
- 3,以任意正有理数为其周期,无最小正周期(由实数的连续统理论可知其无最小正周期)
- 4,处处不连续,处处不可导,在任何区间内黎曼不可积
- 5,函数是可测函数
- 6,函数是周期函数,但是却没有最小正周期,它的周期是任意负有理数和正有理数。因为不存在最小负有理数和正有理数,所以狄利克雷函数不存在最小正周期
黎曼函数:是一个特殊函数,由德国数学家黎曼发现提出,黎曼函数定义在 [0, 1]上。黎曼函数在高数中被广泛应用,在很多情况下可以作为反例来验证某些函数方面的待证命题。
其基本定义如下:

正态分布:
(μ 是期望, σ2 是方差)