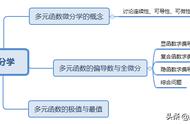
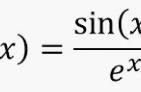标准正态分布:
(μ 是期望=0, σ2 是方差=1)

有界性
设函数 f(x) 在区间 X 上有定义,如果存在 M>0,对于一切属于区间 X 上的 x,恒有 | f(x) | <= M,则称 f(x) 在区间 X上有界,否则称 f(x) 在区间上无界。
奇偶性
设 f(x) 为一个实变量实值函数,若此函数关于 y 轴对称,则称 f(x) 为偶函数。
f(-x) = f(x)
偶函数例子:

设 f(x) 为一个实变量实值函数,若此函数关于原点对称,则称 f(x) 为奇函数。
f(-x) = -f(x)
奇函数例子:

周期性
设函数 f(x) 的定义域为D。如果存在一个正数 T,使得对于任一 x 属于 D 有 (x -T)属于D,且 f(x T) = f(x)恒成立,则称 f(x) 为周期函数, T称为 f(x) 的周期,通常我们说周期函数是指最小正周期。公式如下: