指数函数的定义域是什么,指数函数的值域定义域怎么求

了解到有一些朋友基础不大好，又有想学习的心，所以这一期先写一下指数幂的运算性质和指数函数性质，有了指数函数的基础下一期才能再讲对数函数。

先从运算性质入手，运算性质还需要运用加记忆相结合。

一.正整数指数幂的运算法则

把他推广到分数指数幂也成立，下面来看分数指数幂的运算法则：

二.分数指数幂的运算法则

三.指数函数性质：

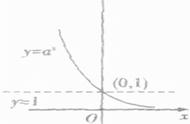
指数函数是重要的基本初等函数之一。一般地，y=a^x函数(a为常数且以a>0，a≠1)叫做指数函数，函数的定义域是 R （全体实数）。注意，在指数函数的定义表达式中，在a^x前的系数必须是数1，自变量x必须在指数的位置上，且不能是x的其他表达式，否则，就不是指数函数。

区别：指数函数的底数a>1时，图像单调递增；底数0<a<1时，图像单调递减；

相同点：图像都位于x轴上方，即函数值都大于0(只会无限接近于0，但永远不会等于0)；所有指数函数都过定点（0,1）。