我们在高中乃至大学都在接触函数,说简单一点,函数其实是一种特殊的映射关系。
定义:一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与之对应,那么我们就称x是自变量,y是因变量,y是x的函数。
理解:函数就像古代皇帝拥有三妻四妾一样,其中因变量 y 就相当于皇帝,三妻四妾就相当于自变量 x ,换句话说,就是因变量y只能有一个,但是自变量x可以是有限个,也可以是无限个。
想必这样说,大家应该很好理解了!那我们今天来学习一个函数里面的子板块,那就是我们今天要接触的指数函数。
在学习之前我来给大家举个例子,我们大家都知道,细胞在分裂过程中,是以一分为二,二分为四,四分为八……一直这样分下去。

那么大家不妨假设一下,如果这个细胞一直按照这个规律去分裂,分裂到n次时,可以得到一组怎样的数?
据观察,这组数如果进行排列的话,可以是以下情况,即(1,4,8,16,32,64,128,…)如果我们将这组数进行转化,那么可以得到一组即相同又不一样的表达,即(2⁰ ,2¹ ,2² ,2³ ,2⁴ ,2 ⁵ ,2⁶,2⁷,…2ⁿ,… )。
通过这一列数字的观察,大家发现没有,这列数的底数永远是2,右上方的指数却在不断增加,大家设想一下,如果底数不变,指数在实数范围内进行变化,那么会得到怎样的情况呢?
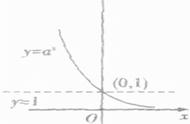
如果按照这个设想一直进行下去,他会得到一条光滑而有规律的曲线,如下所示:

我们再来看个例子,想必大家应该听说过这句话,即:一尺之棰,日取其半,万世不竭,这句话出自于《庄子.天下篇》,意思是说,有一根木棍,如果每天取这根木棍当天的一半,那么不管你取多长时间,都是取不完的。

同样的方法,我们不妨假设这根木棍可以一直这样取下去,并且用数字进行表述,然后将取的数字进行排列观察,即第0天是1,第1天取一半就是½,第2天再取剩下的一半就是¼,依次类推,取到第n天呢?
我们将上述数字进行排列,得到(1,1/2,1/4,1/8,1/16…),将这列数字进行转化,可得[(1/2)⁰ ,(1/2)¹ ,(1/2)² ,(1/2)³ ,(1/2)⁴ ,…(1/2) ⁿ ,…)
通过观察,一直这样取木棍的一半,得到的这组数每一个数,底数永远是1/2,右上方的指数逐渐增加,那么大家设想一下,如果指数在实数范围内不断变化,会得到什么情况呢?