这只是比较特殊的两个例子,如果我们将底数2换成其他的数字,然后固定下来不变动,同样方法,将底数1/2换成其他的分数固定下来,会不会有同样的效果呢?这就是我们这节课要学习的指数函数。
定义:一般情况,像y=aˣ (a为常数,且a>0,a≠1)这样的函数叫做指数函数,函数的定义域是R.
注意:在指数函数的定义表达式中,在aˣ 前面的系数必须是1,自变量 x 必须在指数的位置上,并且不能是x的其他表达式,反之就不是指数函数。
因为a>0且a≠1,所以说底数a的取值要分为两个范围进行研究,当a>1时,有以下图形。

解释:因为在指数运算中,如果底数是负数时,开偶次方根是没有意义的,所以底数小于零时,是一些分散的点,我们研究的是一般情况,所以只规定底数大于零。
根据定义及图像,可以得知当底数a>1时,是单调递增函数,并且必过点(0,1),定义域{x∣x∈R},值域{y∣y>0}
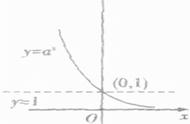
当0<a<1时,有以下图形:

根据定义以及图像,可以得知当底数0<a<1时,是单调递减函数,并且必过点(0,1),定义域{x∣x∈R},值域{y∣y>0}
通过知识点学习,我们来看一个例题:
例题:若函数f(x)=aˣ (a>0,且a≠1)的图象过点(2,16),请确定函数f(x)的解析式。
解答:根据题意,函数f(x)经过点(2,16),所以将该点代入指数函数模型,可得a² =16,解得 a=4 或 a=-4(舍去)。
则函数f(x)的解析式为f(x)=4ˣ

今天的内容就讲到这里,大家下去过后可以做一做上面的练习题,有不同见解的朋友,评论区留言讨论。
,