一、指数函数是怎么来的?
首先我们来看这种形式:

大家都知道上式表示的是n个m相乘这样一种运算结果。
我们通常把这种形式称为“幂”。
蹲在地上的那个m称为底数,肩膀上的那个小点的n称为指数。
到这时候为止,无论m还是n,我们都认定它们是常数,好了,我们现在开始引入变量。
假如我们把底数作为变量,也就是把m换成变量x,上面的幂就变成一个函数,因为随着自变量的变化而幂的值会发生变化。
为了和以后的型式统一,我们把指数写成常数a的形式,就形成了课本上定义过的幂函数的标准形式:

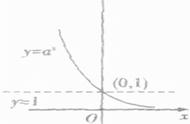
前面我们已经详细介绍过幂函数,我们把指数a这个常量的取值范围扩展到全体实数时,自变量x的取值范围,也就是函数的定义域会受到指数取值的影响。
现在我们换另一种玩法,把底数m换成常数a,把指数n换成变量x,那就形成了另一种幂:

这样,随着自变量x的变化,幂的值也会发生变化。
我们把这种底数为常量,但指数为变量的幂称为另一种函数——指数函数
指数函数的定义: