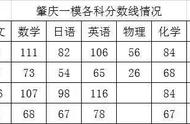
三角函数对照表
但三角函数对照表是近似值,在一些计算精度要求很高的场景,可能并不能满足要求。
三角函数的解析值含义以正弦函数值求法为例,因为求得正弦函数值,就不难求出其他三角函数的解析值。这里的解析值是指精确解(如),而非近似解(如1.41421356237)。
从下文可以看出,1°到90°的三角函数(如正弦函数值)都有解析解,都可以通过正整数的加减乘除、开根号(二次根号、三次根号等)、负号等构成的表达式表示,是精确值,而非三角函数表中的近似值。

求出1°~90°角的三角函数值,再根据三角函数的诱导公式,就不难求出91°-360°角的三角函数解析值了。

根据正弦函数的定义,不难得到:
道生无,无即0。“道”(Tao)即前面的关于正弦函数的定义。
我们就从0出发给出所有1°到89°的正弦函数的解析值(注意是精确的解析值,而非小数的近似值)的求法。
∵,所以
∴
根据正弦函数半角公式,得出:
根据正弦函数的三倍角公式得到:,也即,这个是的一元三次方程。解该方程,得到:,进而得到。

15°角的三角函数值的几何求法: