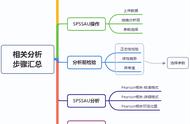
若要运用SCE算法求解有约束的水库优化模型,首先需要解决种群(包括可行解和非可行解)优劣排序问题。SCE算法仅基于目标函数值进行排序,并未考虑个体的约束违反情况,由于目标函数和多个约束之间具有不可公度性和矛盾性,难以将多个约束条件合理地融合至单一目标函数,需要耦合独立的约束处理方法。SR算法简单易行,应用广泛,适用于大多数进化问题,因此,可将SCE算法与SR算法耦合,兼顾考虑目标函数与约束条件,使其适用于有约束的复杂非线性多目标水库优化调度问题。两种方法的耦合方式如图1所示,仅有一个参数pf需要调整。SCE-SR算法具有两个主要特征:(1)确定性方法和竞争进化的结合;(2)随机性方法和复合形混掺排序的结合。前者保留优秀个体,使种群每一次进化都趋向更优的方向,提高全局收敛的效率,后者保证了算法的全局性以及算法的灵活性和鲁棒性,这些特征的结合保证了SCE-SR算法的全局收敛性。
SCE算法中参数的设置影响着优化结果。根据段青云等的研究,SCE算法的一些参数设置如下:(1)每个复合形的个体数,m=2n 1,n为决策变量的维数;(2)每个子复合形的个体数,q=n 1;(3)每个子复合形产生的连续后代个数,α=1;(4)每个复合形的进化次数,β=m。SR算法也有一个参数pf需要设定,RUNARSSON等[15]给出pf建议范围为[0.4,0.5],本文中pf=0.45。
SCE-SR算法终止的收敛条件主要有以下三个。
(1)目标函数值。

(2)变量区间收敛。
当变量所处区间足够小时,停止计算,其表达式为

表2 月平均生态流量区间 m3/s
Table 2 The range of monthly average ecological flow m3/s
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 7 479 | 6 871 | 8 210 | 11 728 | 17 182 | 24 187 | 43 684 | 49 458 | 37 980 | 25 368 | 13 527 | 8 440 |
| 3 627 | 3 159 | 3 083 | 4 234 | 7 321 | 11 183 | 19 035 | 11 394 | 10 957 | 7 953 | 6 595 | 5 001 |

(3)循环次数。
当目标函数调用次数达到预定值时,停止计算。
3 实例研究本文针对三峡水库,以宜昌站流量作为三峡水库下泄流量,因宜昌水文站位于三峡坝址下游44 km, 且控制流域面积接近三峡水库的集水面积。采用张召等确定生态流量适宜区间的水文学法中逐月最小生态径流法确定河道生态流量的上下限值,根据三峡水库1950—2019年的年平均入库流量进行频率计算将相同月份的多年月径流量由大到小排序,同时为了排除偶然性的影响,从中选取次最大值和次最小值,最终形成生态流量区间(见表2),依托丰(频率15%)、平(频率52%)、枯(频率81%)这3个典型年案例(三峡水库3个典型年月平均流量见图3)。出力系数K取8.8,由于枯水年无法满足保证出力,故将枯水年出力保证率设为80%。
SCE-SR算法参数设置如下:模型维数n=12,每个复合形包含样本点数m=25。由于SCE-SR算法的优化结果与复合形个数(p)相关,取p值为8、12、20,以验证不同复合形个数下算法的性能。总样本点数(s=p×m)分别为200、300和500,为保证总样本量相同,遗传算法的种群大小也分别设置为200、300和500。针对不同典型年和复合形个数设定了9个不同工况(见表3),每个工况用遗传算法和SCE-SR算法求解时分别进行30次独立运行。采用5个统计指标来评估SCE-SR算法和遗传算法的优化结果,包括多目标函数转化为单目标后目标值的最大值、最小值、平均值、标准差和寻找第一个可行个体时目标函数调用的次数(NOFCFFI)。前三个指标能直观地反映两个算法优化结果的大小,标准差能展示算法的稳定性及收敛性能,NOFCFFI则与算法的可行域定位能力相关。在计算机条件(CPU为Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz (8 CPUs),内存为8 192 MB)下当模型循环次数100 000次时,遗传算法计算时间大致为2.5 h, SCE-SR算法为3.5 h; 当模型循环次数150 000次时,遗传算法计算时间大致为5 h, SCE-SR算法为6.5 h; 当模型循环次数250 000次时,遗传算法计算时间大致为7 h, SCE-SR算法为8 h。