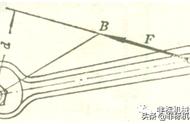
所谓平面汇交力系就是各力的作用线都在一个平面内且汇交于一点的力系。如土建施工起重机吊钩受T1、T2、T三个力作用,这三个力在同一平面内且汇交于一点,这个力系就是平面汇交力系(如图)。
刚性体在三个力作用下处于平衡状态,其中两个力的作用线汇交于一点,则第三个力的作用线必通过该点,三力组成一个平面汇交力系。
平面汇交力系的平衡的必要充分条件是为力系的合力等于零,力系中所有各力在两个坐标轴上的投影的代数和为零。
平面汇交力系的平衡问题可用平面汇交力系合成的解析法厂未解决。根据力的合成与分解法则,平面汇交力系中的各力,可在力系所在平面内分解为沿着任意两个相垂直的坐标轴(x、y)方向的分量。由此可见,平面汇交力系相当于两个正交的共线力系。由共线力系平衡条件可知,物体在x方向不发生移动的条件为:各力在x轴方向的分量的代数和等于零,即∑x=0,同时物体在y轴方向不发生移动的条件为:各力在y轴方向的分量代数和等于零,即∑y=0,于是,物体在平面汇交力系作用下,在x、y两个方向不发生移动的静平衡条件为∑x=0及∑y=0,应用这二个彼此独立的联立方程,可以求解平面汇交力系平衡问题中的两个未知量。平面汇交力系所有力汇于一点,不需要平行移动作用力,如果平面各力不汇交一点,平移各力,需附加力偶才等效。
例:起重机吊钩通过绳索吊起重物G=4000kg,已知两根绳索与铅垂线的夹角为30度,求绳索OA、OB的拉力。吊钩和绳索的重量略去不计。
解:先选取重物、吊钩及吊索OA、OB整个为研究对象,y轴方向的分量,作用在其上面的力有重物重量G和铅垂绳索的拉力T,由二力平衡条件知,T=G=4000kg。
再选吊钩为研究对象,吊钩受三段绳索的作用,其受力图如图所示。根据平面汇交力系的平衡条件得:
∑x=0,T1 sin 30°-T2sin 30°= 0 ①
∑y=0,T-T1cos 30°-T2 cos 30°= 0 ②
由①得 T1=T2 ③
将③代入②得
T=2T1*cos 30°=√ 3T1
由③得 T1=T2=2309kg(绳索OA、OB拉力)

平面汇交力系平衡图
,