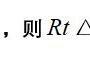在本节我们将了解:
- 内切圆原理
- 证明三角形角平分线交于一点
- 三角形内切圆半径公式
三角形内切圆:与三角形各条边都相切的圆叫做三角形的内切圆。
三角形内切圆的圆心和半径是通过三角形的角平分线交点来确定的。
先复习一下角平分线性质:角平分线上的任意一点,到角两条边的距离相等。

证明如下:
直线AF平分∠BAC,过点F分别作AB和AC的垂线,构成2个直角三角形ΔAGF和ΔAHF
∵ ∠GAF = ∠HAF
∴ ∠AFG = ∠AFH,且两个直角三角形有公共边AF
∴ ΔAGF ≌ ΔAHF(ASA,角边角判定)
∴ FG = FH
证明完毕
以上也等价于:一个点到一个角两条边距离相等,则该点在这个角的角平分线上。
在任意三角形中必然有一个内切圆(也必然有一个外接圆)
过程如下:

- 做ΔABC任意两个角的角平分线,相交与D点。
- 过D点作三角形三条边的垂线,分别交E,H,G。
- 根据角平分线性质可得,DE=DG=DH,这3条线段的长度为内切圆的半径,D点为内切圆的圆心。
- 以D为圆心,DE为半径作圆即可。
通过三角形内切圆,我们可以证明三角形的三条角平分线交于一点。

∵ DG = DH
∴ D点必然在∠ACB的角平分线上
∴ D点同时在三条角平分线上
∴ ΔABC的三条角平分线交于一点
证明完毕
三角形内切圆半径公式: