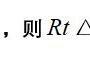三角形三边高与内接元半径的关系
在三角形中有许多量的关系,平时注意累积,当做一些题目时,可能这些潜在的公式就会派上用场。
在三角形中三边的高分别是ha, hb, hc, 三角形的内接圆半径为r.
求证在三角形中满足下列等式,
1/r = 1/ha 1/hb 1/hc

证明: 左侧的三角形的面积等式为
S=aha/2=b/2=chc/2
所以:
1/ha=a/2S
1/=b/2S
1/hc=c/2S
因此:
1/ha 1/hb 1/hc==(a b c)/2S
而右侧三角形的面积为:
S=(ra rb rc)/2,
即
1/r=(a b c)/2S
所以:1/r = 1/ 1/ 1/