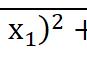罗氏几何中的公理,罗氏几何和欧氏几何区别

欧几里得的《几何原本》是人类历史第一个用公理化方法建立起来的演绎系统

数学公理化的目的, 就是把一门数学表述为一个演绎系统。这个系统的出发点, 则是一组基本概念和若干条基本命题, 基本概念必须是对数学实体的高度纯化和抽象, 基本命题则是对基本概念相互关系的制约和规定。陈述公理化方法的推理基础, 在古典学中多数都是采用自然语言来规定基本概念的定义, 或加入一些特定的符号, 这种语言类似于现代逻辑中的二阶语言(Second-order language)。当今世界, 公理化方法已广泛地应用于数学的各个近代分支, 并且日益向其他自然科学渗透。1978年8月, 在凯尔苏赫(Karlsruhe) 举行的第三届国际数学教育会议上, 当代数学界最高奖菲尔兹(Fields) 奖获得者M.F. 阿蒂亚(Atiyah, 1929 —) 在其论文《纯数学的发展趋势》中, 称二十世纪为数学的“抽象公理化时代”。在这个时代里, 公理化方法不仅是衡量数学纯不纯的标准, 而且也是衡量数学美不美的标准。

古希腊是当时欧洲商业的中心, 在长达一千多年的光辉灿烂的希腊文化中, 数学更加绚丽多彩。在数学发展史上, 最原始最有影响的公理系统, 是欧几里得(Euclid, 约公元前330 — 公元前275) 所建立的初等几何公理系统。这个公理系统乃是他的世界名著《原本》的理论基础。然而, 远在欧几里得之前,在古代巴比伦人、埃及人和希腊人那里, 就已产生了公理化思想的萌芽。公元前六世纪时期, 希腊数学的鼻祖泰勒斯(Thales, 约公元前624 – 公元前547)就把逻辑论证引入于数学之中。及至希伯索斯(Hippasus) 发现无公度线段之后, 毕达哥拉斯(Pythagoras,公元前580 — 公元前497) 学派即逐步认识到直观、经验和实践并非绝对可靠,希望对过去由经验而直接得到的几何知识都能够用严格的逻辑推理来加以证明。

柏拉图(Plato, 公元前427 — 公元前347) 曾经提出:“迫使灵魂用抽象的数来进行推理, 而厌弃在辩论中引入可见的和可捉摸的现象”。(《共和国》) 在这种思想的指导下, 他的门生已开始依据逻辑次序来整理几何定理, 并且引用一些大家公认的原理, 作为推理的基础。这个学派的主要人物铁塔斯(Thextetus, 公元前480 年前后) 和欧多克斯(Eudoxus, 公元前408 — 公元前355)的研究成果, 后来分别被欧几里得收集于《原本》的第十卷和第五卷之中。

亚里士多德(Aristotle, 公元前384 —公元前322) 认为秩序和对称是美的主要因素, 但二者都可以在数学中找到。他是柏拉图学园的一位高才生。他在自己的一些著作中曾经阐述过公理化思想的基本原理, 并且提出:“原理的存在是必须接受的,而其他东西则需要证明”。因此, 很多数学史家都认为数学公理化思想的萌芽始自于亚里士多德的著作。

白俄罗斯共和国列宁大学教师进修学院哲学教研室主任哲学博士茹科夫在《数学的哲学问题》一书中, 把公理学的结构分为三种: 即含内容的公理学、半角式化公理学和形式化公理学。然而, 从公理学的形式化发展之历史过程来看, 这三种公理学亦可称之为是数学公理方法形式化发展的三个阶段: 即产生阶段、完善阶段和形式化阶段。

亚里士多德是古希腊形式逻辑的创始人, 他总结了当时已经积累起来的逻辑知识,以演绎证明的科学(主要是数学) 为实例, 建立了逻辑学的初步体系。由于欧几里德本人也是柏拉图学园里的学生, 并且在里面学习过数学, 因而, 亚里士多德所奠定的形式逻辑以及建立科学体系的方法论原则, 对于欧几里德的数学研究产生了积极的影向。

亚里士多德提出: 公理应为“最普遍的真理”。欧几里德欣然应诺, 并以此作为划分公理与公设的依据。他在建立《原本》的公理系统时, 即是依据逻辑相关性的原则, 先给出点、线、直线、面、平面等一些原始概念的直观定义, 接着又给出由这些原始概念所派生的概念之定义, 如两条直线间的角、直角、平角、圆、直径等, 像这样一连列出23个定义、5条公设和9 条公理。这9 条公理可适用于当时的一切数学, 而5条公设则是专门对于几何学而设立的。

欧几里得以这些定义、公设和公理为基础, 以形式逻辑为工具, 演绎出467个定理,筑起了一座数学知识的大厦—《原本》。正如《欧德摩斯摘要》一书中所说的: “把几何原理联系到一起, 把欧多克斯的许多定理有次序地安排起来, 把铁塔斯的许多定理加以完善化, 并对前人未经严谨证明的许多东西给以无可争辩地阐明的, 乃是欧几里得”。在这个阶段里, 由欧几里得所建立的初等几何公理系统, 就是含有内容的公理学的一个光辉典范。它以体系优美而著称于世, 犹如一座雄伟庄严的科学宝殿, 使后世许多数学家都沉醉于它那迷人的温馨的美的光芒之中。

《原本》的影向和作用, 超过任何一本数学著作, 仅是手抄本就流传了1800多年。自1482年印刷以后, 世界各国的主要语种几乎都有译本, 总印数超过一千版次。两千多年来, 一些著名科学家学习数学时, 大都是以《原本》或其改编本作为入门的阶梯。

现在世界各国的中学几何课本, 仍然受到《原本》的传统影响, 然而, 它的缺陷早已为古代学者们所察觉。由于第五公设排在最后, 应用较少, 而且在陈述上也有些累赘, 致使许多大数学家都试图利用其他公理来证明它, 但其结果都以失败而告终。

十九世纪俄国年轻数学家H.N. 罗巴切夫斯基Lobatchevsky (1793 — 1856) 认真分析了前人的经验与教训, 大胆地提出一个新观念: 可能会存在第五公设不能成立的新几何系统。在这种思想的指导下, 他一举而创立了罗巴切夫斯基几何学, 简称罗氏几何学, 又称为双曲几何学。当时独立地发现这种新几何理论的, 还有大数家K.F. 高斯(Gauss, 1777 — 1855) 和青年数学家L.鲍耶(Bolyai, 1802 — 1860)。不久, 德国数学家G. F. B. 黎曼(Riemann,1802 —1866) 从另一侧面否定第五公设, 又发现了黎氏几何学, 或称为椭圆几何学。这两种几何学统称为非欧几何学。

非欧几何学的建立, 不仅为公理化方法的进一步发展奠定了基石, 而且为新数学理论的发现提供了先例, 接着有许多数学家致力于公理化的研究。在1871 — 1872年, 德国数学家G.康托(Cantor, 1845 – 1918) 和J.W.R. 戴德金(Dedekind, 1831 –1916)不约而同地提出了连续公理。在1882年, 德国数学家M. 巴许(Pasch, 1843 – 1930)出版了《新几何学讲义》, 他在该书中所给出的初等几何公理系统, 前12条相当于日后希尔伯特系统中的I1 — I8 与II1 — II4 , 他定义合同概念所使用的10条公理, 相当于日后希尔伯特系统中的III1 — III5。然而, 该系统不仅是未曾分组, 而且条数也太多, 显然不能给人以简单性的美感! 意大利数学家G. 皮亚诺(Peano, 1858 –1932) 和他的学生M.庇爱里(Pieri, 1860 – 1904)在1889年和1899年, 分别发表了两篇关于初等几何公理系统的论文, 他企图使公理条文的个数达到极少, 以致公理的表述十分冗长, 结果他所提出的系统变得十分庞杂。

德国著名数学家D. 希尔伯特(Hilbert,1862 –1943) 于1899 年出版了《几何学基础》一书,该书被誉为半角式化公理学的代表作, 同时他也是举世公认的“现代数学中公理化方法的奠基人”。他在该书中提出了一个比较完美的初等几何公理系统, 其中包含6个基本概念“点”、“直线”、“平面”、“属于”、“介于”、“合同于” (前3个基本概念一般称之为基本元素, 后3个基本概念一般称之为基本关系), 以及描绘这6个基本概念之间相互关系的20条基本命题。实际上,这20条基本命题即是这6个基本概念的隐定义。对于基本命题,也可称之为公理条文。(参见下表)

希尔伯特的《几何学基础》, 是他一生许多著作中读者最多的一本书。该书之所以能够赢得当时数学界的公认, 乃是因为它的公理系统条数最少、逻辑清晰、结构自然。将其与欧几里德、巴许、皮亚诺等人的有关著作相比, 唯有希尔伯特的杰作才能给人以和谐而简单的美感!

二十世纪初期, 公理化方法使得许多新旧数学分支的逻辑基础得以建立, 并且有可能进一步对各种数学理论统一进行分析与比较。一时间, 许多数学家都在忙于建立新系统, 或者改造旧系统, 这种时髦的活动, 被称之为公理化运动, 这对于当时的数学家具有较强的吸引力!希尔伯特曾经评论道:“对于任何严正的研究精神来说, 公理化方法都是并且始终是一个合适的不可缺少的助手”。

自从希尔伯特的《几何学基础》问世以后, 数学公理化方法立即迅速地向着完全形式化方向发展。当然, 可以想象, 如果没有康托的抽象集合论和数理逻辑的近代发展, 数学公理方法的形式化也不可能获得新的进展。

在当时, 由于公理化方法逐步推广应用于各个数学分支之中, 于是希尔伯特又提出一门新数学, 名叫“证明论”或者“元数学”,它的研究对象, 是专门处理各个数学分支公理化的和谐性问题。

在当时, 由于公理化方法逐步推广应用于各个数学分支之中, 于是希尔伯特又提出一门新数学, 名叫“证明论”或者“元数学”,它的研究对象, 是专门处理各个数学分支公理化的和谐性问题。

通常把希尔伯特的主张, 称为希氏规划,其基本内容如下:

(1) 证明古典数学的每个分支都可以公理化。

(2) 证明每一个这样的系统都具有完备性(Semantical completeness), 即任意一个系统内的可表命题, 均可在本系统内。经过有限步骤得到判定为可证明或不可证明。

(3) 证明每一个这样的系统都是和谐的。

概括地说, 数学公理化方法形式化的基本思想, 乃是采用符号语言把一个数学理论的全部命题变成公式的集合, 然后证明这个公式的集合是和谐的。公理化方法的形式化,不仅推动着数学基础的研究, 而且还推动着现代算法的研究, 并为数学应用于电子计算机等现代科学技术开辟了新的前景。然而, 含内容的公理学在一定场合下, 仍然是一种有用的数学方法, 它的功效和作用, 是不可能完全为形式化公理方法所代替的。欧几里德的初等几何公理系统, 在当前的中学数学教学中仍然具有重大参考价值。除此而外, 还应该看到: 希尔伯特想把全部数学都纳入于公理化方法形式化的宏伟规划中去的愿望, 已经由奥地利数学家哥德尔(G¨odel) 在1931年发表的“不完全性定理”所表明: 那是永远不能彻底实现的。

1933 年在法国出现一个以布尔巴基(Bourbaki) (这是法国历史上一位战功卓著的将军) 为笔名的青年数学家集团,他们用结构主义观点, 写成一本皇皇巨著《数学原本》,从1939 年到1983年, 已经出版40册。从本质上来说, 结构主义乃是形式化公理方法在方法论上的新发展, 形式化公理方法是着眼于探讨每个数学分支的公理化, 而结构主义则是着眼于探讨整个数学大厦的公理化, 他们先从全局上来分析各个数学分支之间的结构差异和内在联系, 然后再对每门数学深入分析其基本结构的组成形式。与形式化公理方法相比, 结构主义则是对数学理论的更高一步、更深一层的抽象和概括。这样做不仅有助于发掘各个数学理论之间的内在亲缘关系, 解除数学理论之中的非本质界限, 而且有助于扩大数学理论的应用范围。

布尔巴基学派提出: 一切数学理论都是集合论的衍伸, 建立在集合论之上的基本结构有三种:即序结构、代数结构和拓朴结构。

这些结构, 统称之为母结构。在任何一个母结构中, 再加入几条补充公理, 就可以得到一些新结构, 这些新结构称为子结构。把几种结构结合起来, 又可以构成复合结构,例如, 序拓朴是序结构与拓朴结构的有机结合, 布尔代数是代数结构与序结构的有机结合, 拓朴群是拓朴结构与代数结构的有机结合。对于这些结构关系的理论体系,可以简单地以下图表示之:

对于数学的定义, 布尔巴基学派描绘得十分风趣, 他们写道:“数学好比是一座大城市, 其郊区正在不断地并且多少有些混乱地向外伸展, 与此同时, 市中心又在时时重建,每次都是根据构思更加清晰的计划和更加合理的布局, 在拆毁旧的迷宫式的断街小巷的同时, 修筑新的更直、更宽、更加方便的林荫大道, 通向四面八方”。现在看来, 布尔巴基学派的工作, 已经深刻地改变了数学的外貌和语言, 他们确实是在数学这个大城市中拆毁了不少“旧的迷宫式的断街小巷”, 他们所建立的母结构、子结构和复合结构, 亦即是新修的一些“更直、更宽、更加方便的林荫大道”, 数学家们在这种“林荫大道”上漫步, 怎不令人陶醉神往!

布尔巴基学派原来设想把数学结构的研究, 从一个分支转移到另一个分支, 直至数学的一些很僻远的领域之中。而现在, 他们已不得不放弃对某些数学领域的探讨, 这不仅是因为数学的进展比《数学原本》的编写更加迅速, 而且是因为整个数学内容实际上比结构主义者最初的设想要复杂得多!今天看来, 这个学派已很难实现他们的全部计划。

上世纪六十年代, 在欧美各国首先掀起了中小学数学教学内容现代化的改革运动, 在这次改革中所出现的各种新大纲和新教材, 都是在结构主义的严重影向下而编写的。因此, 由这次改革而引起的争论, 也涉及到一些对于数学公理化方法的评论。七十年代初, 在美国出版的一本评论专著《为什么小约翰不会计算—新数学的失败》, 该书作者指出: 仅仅强调公理方法,对于数学的发展是不够的; 否认直观, 不仅不可能教好数学, 而且也不可能使数学本身的发展取得本质性的突破。这里所说的正是数学公理化方法在应用上的局限性。

美国数学家F. S. 梅里特在其所著《工程中的现代数学方法》一书中曾经说过: “每一模型都是由一组公理定义的, · · · 公理自身必须无矛盾且相互独立”。所谓一组公理,即是一个公理系统。关于公理系统的无矛盾性, 是指借助于演算不可能在一个公理系统中推出两个相互否定的命题。关于公理系统的独立性, 是指在该系统中任何一条公理都不可能作为其余各公理的逻辑推论。如果一个公理系统具备无矛盾性(即兼容性) 和独立性, 那么, 这个公理系统(或者说这个理论体系) 就是优美的。因此, 兼容性和独立性也就是公理系统的美学标准。

俄罗斯维林金等编着的《中学数学现代基础》一书中曾指出: “可以由给定的公理系统导出的全部不同的命题, 一般说来有无穷多个。因此, 为了证明给定的公理系统的兼容性, 要想由这一公理系统作出全部可能的推论, 并且指出其中没有相互矛盾的命题, 这是不可能的。为了解决这个难题, 曾经创造一种特殊的方法, 它的名称叫做模型法”。所谓模型法, 即是欲证明某一新数学理论的无矛盾性(一致性), 或者欲证明某一新数学理论与某一已知的(旧) 数学理论的兼容性(相对一致性), 可以设法为它在古典数学中构造一个模型, 并且进而证明这个新数学理论的公理系统在该模型中都能够得以实现, 这样, 即可以把这个新理论的兼容性, 化归为新理论与建造它的模型(新理论的模型) 时所需要的古典数学理论的兼容性(相对一致性)。因此, 这种模型法, 又可称之为化归法。例如,我们利用庞加莱(Poincar´e) 模型和球面模型,可以把非欧几何的兼容性, 化归为欧氏几何的兼容性, 再利用算术模型, 又可进一步把欧氏几何的兼容性, 化归为算术理论的兼容性。然而, 对于一个新理论而言, 并不需要如此逐步化归, 一般地说, 只要是在古典数学中, 能够为其构造一个数学模型已足, 因为古典数学已经过亿万群众长期的科学实践检验。

维林金在《中学数学现代基础》一书中指出: “利用模型法也可以解决所给公理系统的独立性问题。如果理论T 中的公理A, 由其它公理既不能证明, 也不能否定, 则称公理A 是与其它公理相独立的。要证明所给公理A 的独立性, 应该建立一个新的公理系统, 在其中将公理A换成它的否定, 而T中其它公理则保持不变。如果所给的公理系统以及用上述方法由它所得到的新公理系统都是兼容的, 那么, 则称公理A与该理论体系T中的其它公理是相独立的”。假设∑为一个公理系统, 并且已证得它是兼容的。令∑ ={A1,A2,A3, · · · ,An}, 欲证其中某一条公理Ai (i = 1, 2, · · · , n) 对于∑中其余各条公理是独立的, 可以先构造一个与Ai 相矛盾

的命题A-i (也可表示为¬Ai), 然后再证明新构造的公理系统{∑′ Ai} 具备兼容性(其中∑′ ={A1,A2, · · · ,Ai−1,Ai 1, · · · ,An}),由此即可推得Ai 对于∑中其余各条公理具有独立性。

该公理系统共有二十条, 按照希尔伯特着《几何学基础》一书中所排列的顺序, 平行公理可记为p18, 而整个公理系统可记为:

∑= {p1, p2, p3, · · · , p20}。

欲证p18对于∑′={p1, p2 · · · p17, p19, p20}是独立的, 可以另构造一个公理系统{∑′ p-18}, 其实这个系统即是非欧几何的公理系统。其中p18 = { 设a 为任一直线, A 为a外的任一点, 在a 和A 所决定的平面上, 至多有一条直线通过A, 但不和a 相交。}, 此为欧氏几何的平行公理。

p-18 = { 设a 为任一直线, A 为a 外的任一点, 在a 和A 所决定的平面上, 至少有两条直线通过A, 但不和a相交。}, 此为罗氏几何的平行公理。

对于欧氏几何的公理系统, 可以表示为∑; 对于罗氏几何的公理系统, 可以表示为{∑ p-18};对于黎氏几何的公理系统, 可以表示为{∑ p-18}。这三种几何学的公理系统都是二十条,所不同的仅仅是平行公理在陈示上的一字之差, 但是, 由此而推演出的几何定理, 则是迥然各异! 例如, 在欧氏几何中可推出三角形的内角和等于π, 在罗氏几何中可推出三角形的内角和小于π, 在黎氏几何中可推出三角形的内角和大于π。

由上述可知, 利用模型法不难证明公理系统{∑′ p18} 和{∑′ p-18} 是兼容的,因而可以断言: 在希尔伯特的欧氏几何公理系统中, 平行公理对于其余各条公理是独立的。事实上, 这即是利用公理系统的兼容性来证明它的独立性。

至于公理系统的范畴性(Categoricity),是指它的任意两个模型都同构。从直观意义上来讲,所谓两个模型同构, 是指它们的元素及元素间的关系与其所研究的问题的性质无关。

近代以来,一些新建立的公理系统, 多数是不完备的。例如, 群、环、域的公理系统, 就是如此。公理系统不具完备性的这些理论, 其特点往往是: 抽象概括性较高, 应用范围较广, 公理系统中基本概念和基本命题的个数较少, 选取模型的自由度也较大。

由于一切数学理论, 都可以以集合论做为基础, 因而, 任何公理系统的无矛盾性, 经过逐步化归, 都可最终化归为集合论的无矛盾性问题。然而, 关于集合论的无矛盾性问题又将如何解决呢? 在第三次数学危机的冲击下, 数学家们积极开展集合论公理化的研究, 设法把集合概念限制为康托在1899 年所提出的兼容的集合。数学家E. 策梅洛(Zermelo, 1871-1953)在1908 年提出了一个集合论公理系统, 后来, 数学家弗伦克林(Fraenkel) 和斯考莱姆(Skolem) 又加以改进, 从此便形成举世公认的ZF 公理系统。

引起数学家们争论的另一个问题, 就是选择公理。这条公理说: 从一族非空集合中各取一个元素, 可以构成一个新的集合。在一个相当长的时间内, 有些数学家希望用ZF系统来否定选择公理, 可是, 1940 年哥德尔(G¨odel) 却出人意料地证明了ZF 系统与选择公理彼此兼容。于是, 到本世纪40-50 年代, 数学家们又普遍倾向于接受选择公理。因而, 在数学大厦里, 现在实际上存在着两种集合论, 即不包含选择公理的集合论(简称ZF系统) 和包含选择公理的集合论(简称ZFC系统)。

由于承认选择公理与不承认选择公理,都可能会引出一些悖论, 因而, 我们必须清楚地看到:今天数学大厦的基础仍然存在一道裂缝, 数学的理论体系尚未达到最终的完善与和谐!

那么, 究竟应该以何种态度来对待数学理论中的悖论问题呢? 布尔巴基学派的态度是“泰然自若”, 他们曾经这样说过: “就像以往曾多次出现过的一样, 将来有朝一日悖论可能会产生, 在悖论突然出现的迅猛打击下,数学一定会保存下来, 其巍巍大厦的主体部分决不会倾毁。为了重新建立无矛盾的体系,人们将继续通过对数学的概念和方法进行调整来克服这些困难, 而系统地采用公理方法,像在《数学原本》中所做的那样, 必然会大大有助于缩短追索悖论产生根源的过程。廿五个世纪以来, 数学家们曾一再纠正他们的错误, 眼看着他们的科学并不因为产生过悖论而变得荒芜贫瘠, 反而日益繁荣昌盛。追思往昔, 默念未来,我们完全有权利感到心宁神怡,泰然自若。”

有人把数学公理系统的建立说得神秘莫测, 甚至加以歪曲, 把公理系统的建立说成是神的意志。很显然, 公理学并非神学, 公理系统乃是对于大量数学知识的抽象概括, 是数学推理论证的出发点, 并非像神学那样极力排斥理性, 把一切根据统统归诸于圣经。

法国数学家R. 笛卡尔(Descartes,1596- 1650) 是近代唯理论哲学的杰出代表,他提出: 演绎法以公理为前提,公理是不需要任何论证的, 只要纯粹的直觉就能理解。在笛卡尔看来, 直觉是一种理智活动, 不只是感性直观活动。他认为通过直觉就能发现作为推理起点的、无可怀疑而清晰明白的概念, 也就是说, 直觉是发现公理的过程或活动。

美籍华人数学家王浩教授在《对哥德尔的反思》的学术报告中曾经提出: 戴德金得到匹亚诺自然数公理系统, 是来自于对自然数列的分析。分析显然是以一种数学直观为基础。王浩教授认为这个事实对于说明哥德尔的公理化理论, 乃是一个最合适的例子, 而哥德尔的公理化理论的主要内容, 则是由分析概念而确定公理。当然, 这种由分析概念而确定公理条文的思维方法, 也并非一朝一夕之功效。往往要经由几代数学家的艰苦的思维劳动, 甚或经过曲折迂回的历史发展过程。以自然数的公理系统而论, 十七世纪, 德国著名数学家J.W. 莱布尼兹(Leibniz, 1646-1716), 曾经利用演绎法一丝不苟地证明了2 2 = 4。2 2 = 2 (1 1) = (2 1) 1 = 3 1= 4他在这个证明中使用了加法的结合律以及2 = 1 1, 3 = 2 1, 4 = 3 1等自然数的定义。到十九世纪中叶, 德国著名数学家格拉斯曼又挑选出一个定义加法和乘法的公理系统。1888 年, J. W. R. 戴德金在其论文《数是什么? 数应该是什么? 》中提出了关于自然数的性质应该接受的六条事实, 并以此作为公理。1891 年G. 匹亚诺(Peano, 1850-1932) 正式在自己的论文中提出了自然数公理系统, 此系统后来被称为匹亚诺自然数公理系统。

德国著名数学家D. 希尔伯特在名著《几何学基础》一书中, 曾经提出: “建立几何的公理和探究它们之间的联系, 是一个历史悠久的问题, 关于这个问题的讨论, 从欧几里得以来的数学文献中, 有过难以数计的杰作, 这个问题实际上就是把我们的空间直观,加以逻辑的分析”。由此可见, 对于空间直观的逻辑分析乃是建立几何公理系统的一般思维方法。

从数学理论的逻辑结构上来看, 不外乎是通过一些元素和关系, 来定义和推演另外的一些元素和关系。然而, 要想对于其中的所有元素和关系都下定义, 并且对于这些元素和关系之间的一切性质都加以证明, 那是根本不可能的。追本求源, 必然会存在有不可定义的元素和关系, 而这些元素和关系, 分别称为基本元素和基本关系, 二者统一称为基本概念。再者, 对于它们的含意和性质, 还必须加以规定, 亦即是对于它们在数学推理和演算中的作用, 还必须加以说明和限制。这种说明和限制的条文, 就叫做基本命题, 或者称之为公理。因此, 在任何公理系统中都必须包含有基本概念和基本命题这两个组成部分, 并且其中的基本命题乃是对于基本概念的定义。由于这种定义并非十分显然, 有时又称之为隐定义。以中国象棋而论, “马走‘日’字, 象走‘田’, 车走直路, 炮翻山”, 这是下棋规则, 也是下棋的公理, 这些公理亦即是对“马”、“象”、“车”、“炮” 的隐定义。1900年, 希尔伯特在巴黎国际数学家代表大会上的讲演中, 曾经明确提出: “在研究一门科学的基础时, 我们必须建立一套公理系统, 它包含着对于这门科学基本概念之间所存在的关系的确切而完备的描述。如此所建立起来的公理, 同时也是这些基本概念的定义”。

任何一个数学公理系统的建立, 都是在该分支的理论发展到比较成熟的阶段才开始酝酿的。数学家从实际问题加工提炼成数学知识, 这是第一次抽象, 而后由已经积累的数学知识, 加工改造成为具有内部逻辑脉络的理论系统, 则需要进一步再抽象。这种再抽象, 即是该数学分支的公理化过程。在这个过程中, 要经由逻辑分析, 把有关形成概念和理论的最根本的要素抽取出来, 而把那些无关宏旨的东西加以扬弃, 这里往往需要分析与综合、演绎与归纳、实验与抽象等科学方法的并举兼施。按照著名数学家阿蒂亚(M. F.Atiyah) 的描述, 建立公理系统的思维过程是: “专心致志地考虑问题的各个方面, 把它们变成公理, 然后研究它们的推论。像物理的情形一样, 认识到形形色色的问题中那些共有的特征, 应该抽出来加以公理化,这是一个经验和判断的问题。最终的严格考验, 就是对原来的数学问题是否有新的认识”。

在建立公理系统时, 由于对基本概念和基本命题的不同选择, 使得同一个数学分支,在不同的时间和地点, 经过不同数学家的抽象思维活动, 也可以建立起形式迥异的公理系统。例如, 就群论来说, 它的很多性质都可以用来作为自己的定义。荷兰数学家H. A.洛伦兹(Lorentz, 1853-1928) 曾举出四十多种关于群的定义。其中每一种定义, 都可以看作是一种公理系统, 因而, 也可以说,群论至少有四十多种不同的公理系统。以欧氏几何而论, 有Euclid 系统、Hilbert 系统、Veblen 系统、Forder 系统、Bachmann系统等, 此外, 在欧氏几向系统中, 将三角形合同公理换以公理“三角形两边之和大于第三边”, 并保留其他一切公理, 这就是闵可夫斯基的“数的几何”(Leipzig, 1896)。尽管如此, 但仍然不可以把公理系统的建立, 误认为是数学家们随心所欲地取舍而致。英国著名数学家M. F. 阿蒂亚曾经郑重地指出: “经常有人说, 现代数学的特点, 就是建立公理系统的自由, 言外之意, 我们不断地为自己发明一些新规则, 搞一些同传统数学问题无关的游戏, 我认为这个观点是错误的”。

1900 年, 希尔伯特在巴黎国际数学家代表大会上讲演时曾经提到: “一门科学基础的稳固是特别具有吸引力的, 对于基础的检验永远是研究者们至关重要的问题…为了成功地研究一门科学的基础, 就必须对于这门理论有深入的理解。只有对于建筑物的基地,有透彻的和细节上的暸解的建筑师, 才有可能为建筑物奠定坚实的基础”。一般地说, 对于一个公理系统, 在细节上的深入理解, 多数是在论著发表以后的岁月里, 例如, 希尔伯特的世界名著《几何学基础》一书, 从1899年的第一版, 到1930年的第七版, 先后作了系列的修正与精炼, 而其中有些细节, 至今仍然有人在探讨和研究。再者, 一个数学分支公理化的完成, 并不意味着是这个分支理论发展的终结, 而是将促使这一数学分支进一步地向纵深方向的发展与开拓!

数学公理化方法是研究数学的重要思维方法, 它对于近代数学和其他自然科学的发展, 起过重要作用和深远影向。关于数学公理化方法的主要作用, 可概括为如下四点:

1. 从欧几里得到“布尔巴基”, 经历过二十多个世纪, 数学的主要支柱和分支, 大多数都进行了公理化, 使得整个数学构成一个庞大、严谨、优美的理论体系。

2. 根据一定水平的公理化要求而编写的具有逻辑演绎体系的数学教材, 既符合于教学和认识过程的规律, 又有利于培养学生的逻辑思维能力, 乃是一种行之有效的措施。

3. 数学公理化方法不仅可以整理和提炼已经积累的数学知识, 使之构成严谨优美和谐的理论体系, 而且可以扩大数学理论和方法的应用范围。这是因为, 如若一个公理系统能够适用于某种对象的集合, 则它的一切推论也应该适用于该对象的集合。再者, 数学家们如欲检验一个数学理论体系是否适用于某种对象的集合, 只需验证该理论的公理系统能否适用, 这样可以减少大量的思维劳动。

4. 数学公理化方法对于现代物理学、理论力学以及其他各门自然科学的表述方法都有重要借鉴作用。戴维· 希尔伯特在第二次国际数学家大会上讲演时曾经指出: “波尔兹曼关于力学原理的著作(Vorlesungen ¨uber diePrinzipe der Mechanik, Leipzig,1897), 提出了数学研究由原子论观点导出连续介质运动规律的极限过程问题…我们还必须试图通过一种极限过程, 从一组公理出发来推出刚体运动的规律… 如果用几何学作为处理物理公理的模型, 那么, 我们首先要试图借助于少量的公理, 来概括尽可能广泛的一类物理现象, 然后再加进新的公理, 逐步地过渡到更特殊的理论”。近年来, 穆尔卡诺夫曾指出: “在狭义相对论的范围内, 关于超光速可能性的最终解决, 没有严格的公理化是不可能的”。

从本世纪四十年代开始, 由于电子计算器的飞速发展和广泛应用, 引起了在数学发展史上由来已久的算法传统的兴起, 致使在纯粹数学中得到广泛应用的公理化方法表现出明显的局限性。

在数学方法中有宏观与微观之别, 公理化方法是一种宏观数学方法, 它的主要功能在于对已经积累的大量数学知识进行加工、整理、改造和重建工作。而微观数学方法则包含有命题形式推理、数学计算等, 其中既有以一定的逻辑推理法则为依据的方法, 也有以某种数学分支所特有的算法技巧为依据的方法。在通常情况下, 数学工作者在解决一个具体问题时, 往往是先从现存的数学宝库中去搜寻适宜的微观数学方法, 而并非首先去求助于某个公理化系统。