有这么一种几何学,它与我们正常的认知不同:它没有平行线,而且三角形的内角和大于180°,但是它被广泛应用于在地球表面研究航海、航空等实际问题中。何以神奇至此?且看下文分解。

图1
黎曼是19世纪德国数学界的一位风云人物。他在1851年所作的一篇论文《论几何学作为基础的假设》中明确提出另一种几何学的存在,开创了几何学的另一片广阔的领域,后来就叫做黎曼几何学,也叫黎氏几何学。黎曼可以说是最先理解非欧几何全部意义的数学家。他创立的黎曼几何不仅是对已经出现的非欧几何(罗巴切夫斯基几何)的承认,而且显示了创造其他非欧几何的可能性。

图2 黎曼
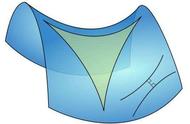
在黎曼几何中的一条基本规定是:在同一平面内任何两条直线都有唯一的交点,这一点的内容形成了黎曼几何不同于欧氏几何和罗氏几何的主要特点。直白的讲,在黎曼几何学中是不承认平行线的存在,过一定直线外一点,永远都不能作“直线"平行于这条定直线。如下图所示,在这个球面上我们把“直线”规定是这个球面的大圆,这样的直线是封闭的,直线可以无限延长,但总的长度是有限的。此外,在球面上任意两点间的距离是过这两点的大圆上介于这两点间比较短的弧的弧长,这也是过这两点的一切弧中最短的弧。

图3
为什么黎曼几何中 “三角形的三个内角和大于180°”呢?我们来做一个直观的理解,请看上图:球面上过北极N和南极S的两条大圆弧(也称子午线)和赤道围成一个三角形,即△NAB。我们知道,子午线是垂直于赤道的,因此,这个球面三角形汇总已经有了两个直角,再加上第三个角,内角和就大于180°了。我们也可以看出黎曼几何与地球之密不可分的关系,难怪它在地表实际问题应用如此广泛了。
在黎曼几何中还有一个特点,就是点和直线、线段和角是“平等”的。怎么理解呢?具体地说,如果我们在任一正确命题中,用“直线”代替“点”,用“点”代替“直线",用“角”代替“线段",用“线段”代替“角”,其余都不变,那么可以得到一个新的正确的命题。比如:直接命题,相异两点确定一条直线。立刻得出另一命题,相异两条直线确定一点。