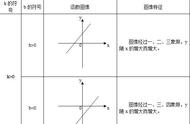
例1解法
牛刀小试解法与例1相同,试试看看。

等角练习
思路(二)如动角,没有一边水平或竖直,用上述方法无法解答时,考虑用下面的方法。
一次函数的综合二次函数求交点坐标,巧解等角问题。
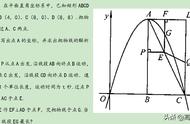
例题如下图:

一次函数求交点,解等角
分析:鉴于BC并非水平或竖直,所以无法用tan∠PBC来列方程求解。
这题考虑用一次函数与二次函数求交点坐标来做,常用方法是构造平行线,对于一次函数来说,平行指的是k值相等。
数形结合如下图:

数形结合
(1)如图位于P1时,构造BP1平行DC,可以先求出DC的一次函数表达式,则BP1的一次函数表达式与它k相等,又因过B点,可求出BP1的一次函数表达式。然后和抛物线解析式联立求出交点P1的坐标。
位于P1时,比较简单。
(2)如图位P2时,介绍两种方法。
方法一:过点C做垂直于BC的直线,分别交BP1,BP2于E1和E点。把E点坐标求出来,再用待定系数法,通过B点和E点坐标,求出BP2的一次函数表达式,然后和抛物线解析式联立求出交点P2的坐标。(不一定非要过点C做垂线,可以取BC上任意一点做垂线,取C只是方便一点。)
关键是怎么求出点E的坐标?
过点C做垂直于BC的直线,分别交BP1,BP2于E1和E点。
两条相互垂直的直线k值的积为-1,可求出CE的表达式,再与BP1的表达式联立,求出交点E1的坐标。
因为∠P1BC=∠P2BC,所以点E和点E1关于C点对称。通过中点坐标公式求出点E的坐标。
强调:两条相互垂直的直线k值得积为-1,为高中知识。
虽然用了高中知识,但这种处理方法比较简单,容易想到。
方法二:利用等腰三角形,三线合一的性质
解法如下图: