(3)

(4)
式中,U表示左奇异向量矩阵;S表示奇异值矩阵;G表示右奇异向量矩阵;γ表示奇异值,γ1>γ2>…>γn>0。由此可得模型参数估值方差

(5)
由式(5)可知,小奇异值导致参数估值方差较大,严重降低了模型参数估计精度[11, 22],TSVD算法通过截掉部分小奇异值来降低方差,提高模型参数估计稳定性,具体表示为

式中,G与U均取前t列向量。


(4)
式中,U表示左奇异向量矩阵;S表示奇异值矩阵;G表示右奇异向量矩阵;γ表示奇异值,γ1>γ2>…>γn>0。由此可得模型参数估值方差

(5)
由式(5)可知,小奇异值导致参数估值方差较大,严重降低了模型参数估计精度[11, 22],TSVD算法通过截掉部分小奇异值来降低方差,提高模型参数估计稳定性,具体表示为

式中,G与U均取前t列向量。

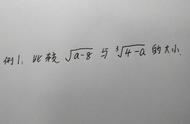














Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.