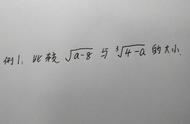(7)
式中,t表示由截断参数确定的需保留的t个较大奇异值。
1.2 常用TSVD截断参数确定方法
影响TSVD解算效果的关键因素是截断参数,最优截断参数可最大程度提高模型参数的估计精度。目前,最为常用的截断参数确定方法有L曲线法、均方误差最小法等。
1.2.1 L曲线法
以log||Xt||为纵坐标,log||AXt-L||为横坐标绘制曲线,通过计算曲线上曲率最大点确定最优截断参数。该曲线形似L,因此称作L曲线法。L曲线法的核心是认为L曲线上曲率最大点对应的截断参数即是最优的截断参数[21, 26]。
令η=log||Xt||,ρ=log||AXt-L||,则L曲线曲率可计算为

(8)
式中,ρ′、η′为一阶导数,ρ″、η″为二阶导数,以不同截断参数计算L曲线曲率,曲率最大点km对应的截断参数即为最优截断参数。L曲线法缺乏合理的理论依据,所确定的截断参数稳定性较好,但难以给出最优的截断参数。
1.2.2 均方误差最小法[22]
均方误差是模型参数估值与真值之间差值的数学期望,反映了参数估值相对于真值的离散程度。TSVD模型参数估值均方误差可表示为

式中,Mt表示均方误差;E表示数学期望运算;

由式(9)可见,均方误差的计算需要模型参数的真值,但实际应用中,参数真值是未知的。鉴于此,均方误差最小法以模型参数估值代替真值计算均方误差。第1步,利用TSVD方法截掉1个最小奇异值获得模型参数初步估计值;第2步,以初步估值代替真值计算不同截断参数下的均方误差,由最小均方误差确定最优截断参数,再次估计模型参数,得到该截断参数下的模型参数估值;第3步,将模型参数第2步估值替代真值重新计算不同截断参数下的均方误差,确定最优截断参数,如此迭代计算,直至两次模型参数估值二范数收敛到某一较小值[22]