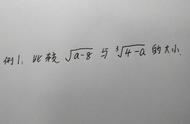(10)
然而,以估值代替真值计算的均方误差并非实际的均方误差,由此确定的截断参数受初值影响较大,常导致迭代过程不收敛或收敛于初值,限制了截断参数确定可靠性。
1.3 改进TSVD截断参数确定方法
1.3.1 截断参数确定方法
有偏估计均方误差由方差与偏差两部分组成,TSVD通过截掉小奇异值来降低方差,但截掉小奇异值导致模型偏离,引起模型参数估计偏差。TSVD模型参数估计均方误差可扩展为[22]

式中,Tt为TSVD模型参数估值方差总和;bt为估值偏差。通过奇异值分解,方差与偏差可表示为

(12)

(13)
式中,gi表示右奇异向量矩阵的第i列向量。
由式(12)和式(13)可知,TSVD每截掉1个小奇异值后,方差的减少量和偏差的增加量不尽相同。在截掉小奇异值后,方差的减少大于偏差的增加,则均方误差会降低,参数估值精度得到提高,估值更接近于真值。因此,判断某小奇异值是否需要截掉的关键在于该奇异值截掉后,方差减少量和偏差增加量的大小关系,即