解:∵∠AOC ∠AOF ∠DOF=180°(平角定义)又∵∠AOC=65°,∠DOF=50°(已知)
∴∠AOF=180°-65°-50°=65°
∴∠BOE=∠AOF=65°(对顶角相等)
例2、如图,直线AB上有一点O,∠AOD=44°,∠BOC=32°,∠EOD=90°,OF平分∠COD。求∠FOD与∠EOB的度数。

解∵∠AOD ∠COD ∠BOC=180°
∠AOD=44°,∠BOC=32°(已知)
∴∠COD=180°-44°-32°=104°
∵OF平分∠COD(已知)
∴∠FOD=1/2∠COD=1/2×104°=52°
∵∠AOD ∠AOE=∠EOD=90°,∠AOD=44°(已知)
∴∠AOE=90°-44°=46°
∵∠AOE ∠BOE=180°(邻补角定义)
∴∠BOE=180°-46°=134°
2、两直线被第三直线所截所形成的角之间的关系:同位角、内错角、同旁内角。

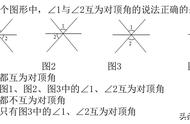
同位角:如图中∠1与∠5位于截线AB的同侧,被截两直线CD、EF的同上方,这两角的位置关系为同位角。
注意:同位角定义中的两个“同”,截线的同侧,被截两直线的同方。依照定义你能找出题中其余的同位角吗?
∠2与∠6,∠4与∠8,∠3与∠7。
内错角:如图中∠2与∠8,位于被截两直线CD、EF之间(内),截线AB的两侧(错),这两个角的位置关系为内错角。
注意:内错角定义中的“内”是指两角被被截两直线夹着,“错”是指两角位于截线的两侧,被截线分开。
图中的∠3与∠5也是内错角。
同旁内角:如图中∠2与∠5,位于截线AB的同一侧(同旁),被截两直线CD、EF之间(内),这两角的位置关你为同旁内角。
注意:“同旁”是指两角位于截线的同侧,“内”指被截两直线之间。
特别注意:如何分清截线和被截直线,可通过找两角的边来确定。这两个角的“公共边”所在直线是截线,另两边所在直线是被截直线。如果两个角没有公共边,则两角不会是同位角、内错角、或同旁内角。

例1:如图(1)中,∠1和∠ABC是直线______,_____
被直线_____所截而成的______角。
分析∵∠1和∠ABC的公共边所在直线是直线BD,其余两边所在直线是AB,EF。它们位于被截两直线AB,EF的同右,截线BD的同上。
∴是直线AB,EF被直线BD所截形成的同位角