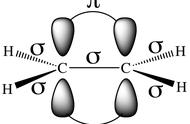
这个例子能看出链接苯环和烷烃的亚甲基C-(CB)(C)(H)2和一般的亚甲基C-(C)2(H)2是不一样的。
该方法的缺点:
使用基团加和法得到的计算结果的准确程度取决于导出基团贡献值的热力学实验数据的准确程度。
一些定义相当含糊的官能团,如偶氮和肟,其基团贡献值也被发表出来。通常包含这类基团的化合物的实验数据很少,所以在使用这些基因贡献值的时候应该特别小心。
基团加和法忽略了基团间的相互作用,这些作用有时候对生成热也有不可忽视的贡献。这里有一些基团加和法失败的例子,其失败的原因不是由于缺乏足够的热力学实验数据,而是因为对基团之间的相互作用考虑不周。
另外要提的参数,比如“生成熵”,它也可以用上面的方法做出“基团加和法表”,但它讨论少的原因是可现有的可参考的数据太少了;还有热容Cp,它可以反应焓变随稳定的变化,化工行业中也很常用。
2.1.7 张力能既然使用化合物的标准生成热来明确定义化合物的稳定性,现在就可以讨论张力这个概念。在本章的开头引入了张力的概念。这就是为什么本段说了那么多有的没的。
张力是由于分子内的化学键、结构或构象的扭曲而产生的内部应力。如果有办法预测一个不存在任何键扭曲的分子的稳定性,也就可以为张力能给出一个精确定义。
基团加和法可以被用来计算有机分子的标准生成热,在此方面它的确是一个很强大的工具。

上图中的偏差来自于小的环系是存在张力的。环戊烷分子在某种程度上存在张力,环丁烷和环丙烷分子内的张力就更大一些。这种张力部分来源于环上的C-C-C键角相对于标准的C-C-C键角发生的明显扭曲。(其实Benson及其合作者已经把这一研究进一步扩展到包括杂原子和不饱和的化合物有关基团的贡献值及环状化合物的修正值。)
基团加和法当然没有考虑环内的张力。因为这种方法在参数化的时候仅仅考虑一些简单的、不存在成键扭曲的非环烷烃,所以它不适用于环烷烃。
我们网此可以明确定义张力能的概念——张力能就是一个分子由实验测定的标准生成热与用基团加和法预测的标准生成热之间的差值。
我们可以尝试着把张力能分解为键角张力、二面角张力和环张力等,将在本章中对此进行讨论。这种做法从原则上讲是非常危险的。因为如果用量子力学来描述化学键,将不能自然而然地导出以上这种对张力能的划分方案。所以必须进行人为的划分。事实上这也是很有用的策略,但是我们在应用它的时候一定要谨慎。

March里的这张图比较直观,所以贴过来了,但注意不同的书张力能定义不一样,March的图只是给了一个笼统的说法。