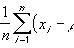这里,残差的头上也有一个“^”(hat),意味着残差也有总体与样本之分。由上面残差的计算公式也可推知这一点,因为预测值有样本与总体之分,所以残差也自然也是有的。
我们做线性回归的时候一般需满足:
1)线性(L):因变量与自变量之间呈线性关系;
2)独立(I):各观测值相互独立;
3)正态(N):自变量(X)固定时所对应的因变量(Y)服从正态分布;
4)方差齐(E):不同自变量取值下因变量的方差相等。
以上四个条件即俗称的LINE条件。这些条件虽然是针对因变量而言的,但我们却可以通过对残差进行分析达到检验的目的。一般而言,如果残差满足以上四个条件,则称线性回归的假设条件得到满足。
(有关回归诊断的问题,后面我们会专门详细介绍。)
回归分析的预测值
看完残差,我们再来看看预测值。这里要指出回归方程的第三种写法(一般对于总体回归):

看到 μ第一反应应该是均数,而且是总体均数(非样本均数),所以 μγ在相关教材上被称作“X取某个特定数值时,Y的条件总体均数”。
这里的“条件总体均数”估计会看晕不少人。所谓“条件”,意味着Y的取值是依据X的取值而定的,“X的取值”是确定Y的前提条件。
由此,严格来说, Ý应该是 μγ 的预测值。
这意味着给定X的取值,我们通过回归获得的是Y的一个平均值。比如前面文章中谈到的教育程度(X)和收入(Y)的回归方程:

当X=15时,可以计算得出 Ý=5000,严格来讲,这里算出的5000并非是某个人的具体收入,而是一群接受了15年教育的人,其收入的平均数。
因为即便是大家都接受了15年教育,但收入也并不完全相同,有的可能一两万,而有的也可能一两千。而我们通过回归获得是收入(Y)在教育程度为15年(X=15)的一个平均数。
理解了这一层,再看下面这图应该会比较轻松。