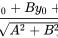直线斜率差异显著性检验（显著性差异字母标记结果怎么分析） - 原点资讯

Significance F<0.05, 说明模型在统计学上是显著的，线性在统计学上是成立的。反之F>0.05, 则说明线性在统计学上不成立。

c. 置信区间：

直线斜率差异显著性检验,显著性差异字母标记结果怎么分析(13)

Coefficients为线性系数a, b值。第一行为线性方程的截距，第二为线性方程的斜率。假如，则a= - 0.2520, b = 1.0291;
标准误差表示为计算a, b时在实验条件下的计算误差；
P-value，第一行P>0.05, 表示b值过原点，标准误差0.2149只是代表测量误差。斜率p<0.05, 表示斜率有统计学意义。
95%置信区间，代表a, b的置信区间。该值可以用来判断多次线性是否发生变化。如果置信区间不变，说明多次线性是一致。

d. 标准误差分析：

直线斜率差异显著性检验,显著性差异字母标记结果怎么分析(14)

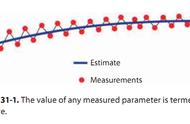
标准误差是指无法准确测试的那一部分数据，即噪音。标准残差可以看作为标准误差的观测值。一般可以用标准误差来估算定量限和检测限。即10´标准误差/斜率公式计算定量限，3´标准误差/斜率计算检测限。标准误差还可以用来评估离群值。

当标准残差绝对值大于2时，说明该测试点异常。

2. 两条回曲线的比较

在分析实践中，遇到同一台仪器在不同时间，或不同人员用相同方法对同一测量对象测量得到两条回归直线不一定相同，包括两条回归直线的标准差不同，或斜率不同，或截距不同。那么如何判断两条回归直线之间是否有显著性差异，两条回归直线是否可以合并后计算测量结果。我们可以用F检验来判断两条回归直线是否一致。

方差分析检测两回归直线的方差是否有显著性差异。

假设两条回归直线为：

用F检验检查两回归线是否有显著性差异，统计量为：

S1､S2为两条回归直线的标准偏差。、为两回归直线的方差。标准偏差可以通过前述方法2中EXCEL软件计算得到。通常将小的方差设为分母，方差分析的自由度为n-2，计算得到F值，与F0.05(n1-2, n2-2)对比，如F< F0.05(n1-2, n2-2)，则表明两直线间无显著性差异，可以合并使用。