1.一元函数伸缩变换推导
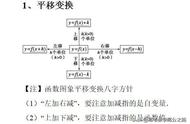
我在前两篇文章中介绍过一元函数图像的平移变换、轴对称变换和中心对称变换。还有一种常见的变换,那就是图像伸缩变换,我先来推导一下一般函数y=f(x)的伸缩变换的表达式。
伸缩变换的就是函数图像的走势不变,在横向和纵向上进行一个方向或两个方向的拉伸或压缩。假设函数y=f(x) 的图像在横向上伸缩为原来的m倍,在纵向上伸缩为原来的n倍,原函数上任意一点(x0, y0)平移之后对应到点(x, y),那么


上式即为一般函数伸缩变换后的函数表达式。当m>1时,函数图像在横向上拉伸为原来的m倍;当0<m<1时,函数图像在横向上压缩。当n>1时,函数图像在纵向上拉伸为原来的n倍;当0<n<1时,函数图像在纵向上压缩。
2.一般形式正弦函数图像的变换y=sin(x)是最简单的正弦三角函数,更一般的正弦函数和余弦函数的表达式如下