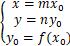得函数者得高考,函数是高考的主线。图像的三大变换规律——平移变换、对称变换和伸缩变换——是揭示函数变化、化繁为简的重要解题方法,下面将其变化规律和在椭圆大题中的应用技巧归纳如下:

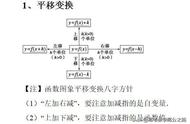
1.平移变换
(1)左、右平移变换:函数y=f(x a)的图象是由函数y=f(x)的图象经过左、右平移得到的,当a>0时,向左平移|a|个单位长度,当a<0时,向右平移|a|个单位长度。
(2)上、下平移变换:函数y=f(x) b的图象是由函数y=f(x)的图象经过上、下平移得到的,当b>0时,向上平移|b|个单位长度,当b<0时,向下平移|b|个单位长度.
2.对称变换
(1)函数y=f(x)自身的对称:
①y=f(x)为奇函数时,y=f(x)的图象关于原点对称;②y=f(x)为偶函数时,y=f(x)的图象关于y轴对称;③若f(x a)=f(-x b),则y=f(x)的图象关于直线x=(a b)/2对称.
(2)函数y=f(x)的图象与下列函数图象的关系:
①y=f(x)的图象与y=f(-x)的图象关于y轴对称;②y=f(x)的图象与y=-f(x)的图象关于x轴对称;③y=f(x)的图象与y=-f(-x)的图象关于原点对称;④y=f(x)的图象与y=f(2m-x)的图象关于直线x=m对称;⑤y=f(x)的图象与y=2n-f(x)的图象关于直线y=n对称;⑥y=f(x)的图象与y=2n-f(2m-x)的图象关于点(m,n)对称;⑦y=|f(x)|的图象是将y=f(x)的图象在x轴下方的部分翻折到x轴上方,其余部分不变而得到的;⑧y=f(|x|)的图象是将y=f(x)的图象中x≥0的部分作出,再由偶函数的图象关于y轴对称作出x<0的部分而得到的.
3.伸缩变换
(1)y=Af(x)(A>0)的图象,是把y=f(x)的图象上所有点的纵坐标变为原来的A倍(横坐标不变)而得到的.
(2)y=f(ax)(a>0)的图象,是把y=f(x)的图象上所有点的横坐标变为原来的1/a倍而得到的.
4.坐标系平移
如果坐标系原点从(0,0)移到(h,k),则函数y=f(x)变为y k=f(x h)。

经典例题:[2017全国新课标Ⅰ卷理科第20题]


代入mx ny=1整理得x-2 2n(x y)=0,
即平移后的直线过定点(2,-2),所以平移前的直线过(2,-1)点。
总结:高考题每年总会常考常新,运用不同的方式设置解题难点,运用好数形结合的数学思想,掌握好函数图像的变换规律,就可以化繁为减、化陌生为熟悉,快速做题,事半功倍。