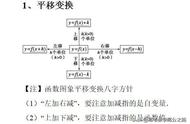
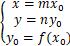函数图象的变换是学生学习函数图象中的难点,也是掌握函数有关性质的难点,同时也是学生易混和不易掌握的基本概念.高考每年都有体现,下面就函数的几种简单变换,作一简单介绍.
一、函数y=f(x)与函数y=f(- x)的图象间关系函数y=f(一x)的图象是由y=f(x)的图象经沿y轴翻折180° 而得到的.注意它与函数y=f(x)满足f(x)=f(- x)的图象是不同的,前者代表两个函数,后者表示函数y=f(x)本身是关于y轴对称的.
二.函数y=f(x)与函数y=f(x土a)(设a>0且为常数,下同)图象间的关系函数y=f(x十a)的图象是由函数y=f(x)的图象向左平移a个单位而得到的,而y=f(x- a)的图象是由函数y- f(x)的图象向右平移a个单位而得到的.
三、函数y=f(x)与函数y=f(a- x )图象间的关系函数y=f(a- x)的图象是由函数y= f(x)的图象经由y轴翻折180°后(注意是y=f(一x)),再向右平移a个单位而得到的(f(a一x)=f[- (x- a)].
四、函数y=f(a x)与函数y=f(a- x)图象间的关系由上面二、三可知:函数y=f(a x)的图象与函数y=f(a- x)的图象关于y轴对称.
五、函数y=f(x)满足f(a x)=f(a- x)时的图象函数y=f(x)满足f(a x)=f(a- x)时,函数 y=f(x)的图象本身关于直线x= a成轴对称图形这里要注意区别y=f(a x)与y=f(a- x)间的关系,y=f(a x)与y=f(a- x)代表两个不同的函数,而满足f(a x)=f(a- x)时,说明函数y=f(x)自身具有的性质,是一个函数而不是两个函数.
六、函数y=f(x)具备性质f(a x)=f(x- a)时的图象函数y=f(x)满足f(x a)=f(x- a)时,说明函数y= f(x)的图象具有周期性,且周期为T=2a,这是因为f(2a x)=f[a (a x)]=f[(x a)- a]=f(x).
七、函数y=f(x- a)与函数 y=f(a-x )图象间的关系由二、三图象可知:函数y=f(x- a)的图象 与函数y=f(a- x)的图象关于直线 ,x=a对称.
八、函数y=f(x)满足f(x - a)=f(a -x)时的图象满足f(x- a)=f(a- x)的函数y=f(x)是偶函数,图象关于y轴对称.f(x)=f[(x a)一a]=f[a-(x a)]=f(- x)或f(x一a)=f[一(a一x)]=f(a-x).
九、函数y=f(x)满足f(a一x)=- f(a x)的图象满足f(a- x)=-f( a x)的函数y= f(x)的图象关于点( a,0)对称.
十、函数y=f(|x|)与y=f(x)图象间的关系y=f(|xl)是偶函数, 其图象是y= f(x)图象在y轴右侧图象部分(含y轴上的点)沿y轴翻折180后共同组成的图象,y=f(x)在y轴左侧部分图象不在y=f(|x|)图象上.
十一、函数y=f(x)与y=|f(x)|图象间的关系函数y=lf(x)|的图象是由函数y=f(x)的图象在x轴上方部分与x轴下方部分经翻折180°到x轴上方共同组成的图象.
十二、函数y=f(x)与函数y= af(x)及y=f( ax )图象间的关系函数y= af(x)的图象是由函数y= f(x)的图象上横坐标不变,纵坐标扩大( a>1)或缩小(0<a<1)a倍得到的,函数y=f( ax)的图象是由y=f(x)的图象纵坐标不变,横坐标扩大(0<a<1)或缩小(a>1)1/a倍而得到的.
,