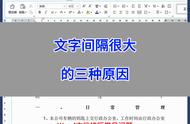
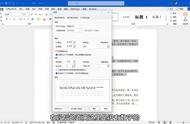
这个公式告诉我们,如果你取所有完全平方数并将它们的倒数和相加,你将会得到\pi^2/6。这是欧拉首先证明的。注意到这个式子只是在前面的第二个方程(欧拉乘积公式)中令s=2。后者是黎曼ζ方程,因此我们可以说ζ(2)的值是π²/6。
9. 调和级数

这个公式有点反直觉,因为它告诉我们,如果你把一些不断变小的数(最终趋向0)加起来,最后将会得到无穷。可是如果你是取它们的平方,和却是一个有限的值(答案是π²/6)。如果仔细观察调和级数,你会发现它正是ζ(1)。
10. 素数计数公式的显式表达

这个方程的重要性体现在:
素数是那些除了1和它本身以外没有其它因子的数。小于100的素数有2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97 。 由此可知,素数的出现没有显然的规律:对于一串连续正整数,有时候你会找到许多素数,有时候你会一个也找不到。找到很多或一个找不到似乎是完全随机的。
很长时间以来,数学家都在尝试给出素数分布的规律。上面的公式正是不大于一个给定数素数个数的显式表达。
以下是各个符号的意义:
π(x): 素数计数函数。它给出了不大于一个给定数的素数个数。例如,π(6)=3,因为有3个素数不大于6:2,3,5。
μ(n): 莫比乌斯函数。它依据n的质因数分解而取值为0, -1或1。
Li(x): 对数积分函数。它被定义为函数1/lnt从0到x的积分。
ρ: 黎曼ζ函数的任意非平凡零点。
令人吃惊的是,整个公式的结果总是一个精确的正整数!这说明,给定一个实数,我们可以把它代入公式并得到不大于它的素数个数。存在着这样一个公式的事实说明,素数的分布存在某些规律,只是我们现在还不能理解罢了。
关注*DuoDaaMath每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
,