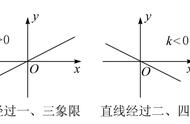
这三个式子,这三个方程说的是同一件事,有时候正比例关系不是那么清晰,但如果进行这样的分析,会分析出相同的结论,或者也可以用代数变换变成这种形式。还有另外的方法,同时在方程两边除以-3,得到-1/3y等于x,这就有意思了,这表明x随着y的变化而变化。
或者可以说x等于常数k乘以y,通常来说这也没错。如果y与x是正比例关系,也可以说x与y是正比例关系,比例常数是不同的。实际上两种情况的比例常数互为倒数,但仍然是正比例关系,这一大套都是正比例。

来研究一下反比例关系,反比例-1它的一般形式,如果还是用同样的变量,当然不一定非得是y和x,也可以是a和b或者m和n。如果说m与n是正比例,那么m就等于某常数乘以n。
现在来看反比例,如果还是用y和x,那么y等于某个常数乘以1/x,不是常数乘以x而是常数乘以1/x。我来举一些例子,y等于1/x,也可以是y等于-2除以x,也就是2/x,也可以是y等于-3乘以1/x,也就是1/3x,也可以是y等于-2除以x。

来研究一下反比例关系,就用研究正比例关系的方法,来选--我看看,选y等于2/x,画同样的表格,画好了,这是x值,这是y值。当x等于1,y等于2,当x等于2,y是2除以2等于1。所以如果x乘以2,《增至2倍,y会如何?y会缩小至1/2,也就是除以2。
注意其中的区别,在这里不管放大缩小,x怎么变化,y也一样怎么变化。而现在是反比例关系,当把x放大一个系数,y会缩小一个同样的系数,这就是"反"比例的意思。或者也可以这样,如果让x等于1/2,如果缩小x,y就要放大,因为2除以1/2等于4,所以放大了y,它俩做了相反的动作,它俩是反比例关系。
试一下负数的情况,也是同样,这里是乘以2,同样,你未必会刚好见到这个形式,它可以变成很多种形式,但同样都描述了反比例关系。只要在代数上等价,你可以把这个式子的两边同时乘以x,然后得到xy等于2,这同样是反比例。

如果画表格的话,跟之前这个不会有区别,也可以两边同时除以y,得到x等于2/y,也就是2乘以1/y。注意,它的意思是y与x是反比例关系。而通过代数变换,也能说明x与y是反比例关系,y与x是反比例关系,也就等价于--用下面这个例子说明了x与y也是反比例关系。
还有把这里两边同时除以2,得到y/2等于1/x,各种各样的古怪形式。所以一般来说,如果有表达两个变量关系的式子,然后问你这是正比例还是反比例,或者都不是?可以像这样画表格,如果把x放大一个固定倍数,y也放大了一样的倍数,那么就是正比例关系。
如果放大x--当然要试多个不同的倍数,而y是缩小的,同比例缩小,那么这很可能就是反比例关系。而最有把握的办法还是用代数变换把式子变成这种形式,这就肯定是反比例关系,或者这种形式,这就肯定是正比例关系。