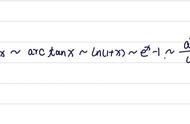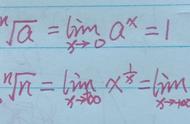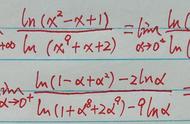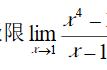无穷小是微积分中的一个重要概念,它指的是当变量趋于某个点时,
函数值趋于零的极限。比较无穷小和无穷小的等价代换是微积分中的基本运算方法之一。
首先,我们来看看如何比较无穷小。
假设有两个无穷小量x和y,我们可以比较它们的大小。
方法是将它们表示成泰勒级数的形式,然后比较它们的系数。如果x的系数比y的系数小,则x比y更小;如果x的系数比y的系数大,则x比y更大;如果它们的系数相等,则它们的阶数是相同的。
例如,考虑x=sin(1/x)和y=cos(1/x),当x趋于0时,它们的值都趋于0,但x的阶数比y高,因此x比y更小。

接下来,我们来看看无穷小的等价代换。
在微积分中,我们常常需要将一个复杂的表达式简化为一个更容易处理的表达式。
通过使用无穷小的等价代换,我们可以将一些复杂的表达式简化为更简单的形式。
例如,考虑f(x)=sin(ax)/x,当x趋于0时,这个表达式的值趋于0。但是,如果我们使用等价代换sin(ax)≈ax,则可以将f(x)简化为f(x)=a/2 O(x^2),这个表达式更容易处理。
在实际应用中,无穷小的比较和等价代换是非常有用的工具。
它们可以帮助我们更好地理解函数的性质和行为,以及更好地解决微积分中的问题。
例如,在求函数的极限时,我们可以使用无穷小的比较来确定函数的极限值;在求解微分方程时,我们可以使用无穷小的等价代换来简化方程的求解过程。
总之,无穷小的比较和等价代换是微积分中的重要概念和方法。
它们可以帮助我们更好地理解函数的性质和行为,以及更好地解决微积分中的问题。
因此,在学习微积分的过程中,我们需要深入理解这些概念和方法,并学会如何运用它们来解决实际问题。