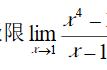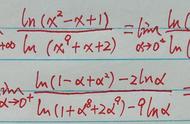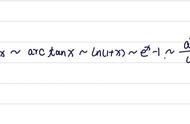上一期我们介绍了极限定义的正确理解以及利用极限定义进行证明的题。可以参考
这一期我们讲极限计算的方法之一:洛必达法则求极限。
大家都知道,两个无穷小量之比或两个无穷大量之比在给定的极限过程中,随着这些无穷小量或无穷大量类型的不同,可以有完全不同的变化状态。因此不能对这样的比的极限作一般性的结论。通常称这种类型的极限为“未定式”。值得注意的是,这里“未定”两字只是意味着关于它的极限不能确定出一般的结论,而并不是在具体情况下的极限总是不确定的.
洛必达法则就是这种未定式的一种定值的方法.
用洛必达法则求极限,其特点是通过求极限号下分式的分子、分母的导数(一次或多次)的方法达到消去未定因素的目的。该法整齐划一,具有很大的一般性,是求解0/0型或无穷/无穷型未定式的使用最广泛的有效方法。
但洛必达法则并不是“万能”的, 下面介绍利用该法则求极限的几种方法与技巧,其中最常用的方法与技巧是把求极限的多种方法与技巧综合运用。只有这样,才能使运算简捷,达到运用自如的境地。
本期主要内容:
一、重要极限 洛必达法则求极限
二、无穷小等价代换法 洛必达法则求极限
三、及时分离非零极限的因式 洛必达法则求极限
四、先变量代换 洛必达法则求极限
五、恒等变形 洛必达法则求极限
六、∞-∞、0·∞转化成0/0与∞/∞ 洛必达法则求极限
七、幂指函数先取对数 洛必达法则求极限
八、0/0与∞/∞的数列极限 间接使用洛必达法则
九、多次使用洛必达
十、利用带佩亚诺余项的麦克劳林公式(泰勒公式)快速光速求极限
十一、洛必达法则越算越繁?不适用——寻求他法
以下十一道例题分别对应上述方法:(为了方便不再打字,直接从本人笔记本截图)




需要注意的是求极限的方法太多,而洛必达法则仅仅是其中的一种,而且洛必达法则由于其局限性有时也需要结合其他方法共同求极限。后期我们会推出夹逼准则求极限、递推关系求数列极限、等价无穷小计算极限、直接代入法等等方法,欢迎持续关注。建议收藏再看,欢迎将原文分享给同学。
,