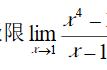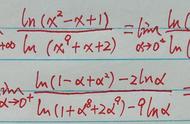数列的极限是数学分析中的一个重要概念,它描述了数列在无限远离零点时所趋向的值。
极限的定义可以追溯到早期的数学分析,它提供了求解某些数学问题的有力工具。
本文将介绍数列极限的定义、性质以及常见的极限类型和计算方法。
一、数列极限的定义
定义:设{an}为数列,a为实数,若对于任意给定的正数ε(不论它多么小),总存在正整数N,使得当n>N时,有|an-a|<ε,则称数列{an}收敛于a,记作lim an=a,或称{an}的极限为a。
二、数列极限的性质
1. 有界性:如果数列{an}收敛于a,则数列{an}有界。即存在常数M>0,使得对于所有n,都有|an|≤M。
2. 唯一性:如果数列{an}收敛于a,则其极限值是唯一的。
3. 保序性:如果数列{an}收敛于a,且对于所有的n,都有an≤bn,则数列{bn}收敛于a。
4. 稳定性:如果数列{an}收敛于a,且对于所有的n,都有an=bn(b为实数),则数列{bn}收敛于a。
5. 夹逼定理:如果数列{an}、{bn}和{cn}满足a≤an≤b≤bn≤c≤cn≤d,且lim an=lim bn=lim cn=d,则lim an=lim bn=lim cn=d。
三、常见的极限类型和计算方法
1. 零点定理:如果函数f(x)在区间[a,b]上连续,且f(a)*f(b)<0,则存在c∈(a,b),使得f(c)=0。这个定理可以用来证明函数在某个区间内有根的存在。
2. 夹逼定理:如果数列{xn}、{yn}和{zn}满足x≤xn≤y≤Zn≤z≤zn≤w,且lim xn=lim yn=lim zn=w,则lim xn=lim yn=lim zn=w。这个定理可以用来证明数列的极限存在。
3. 等价无穷小替换:在求极限的过程中,如果两个无穷小的量是等价的,那么它们可以互相替换。常用的等价无穷小替换包括:sinx~x,tanx~x,ln(1 x)~x等等。这些替换可以使计算更加简便。
4. 洛必达法则:当两个无穷小量之比的极限为零时,如果这两个无穷小量分别对应于函数f(x)和g(x),那么可以应用洛必达法则来求解f'(x)/g'(x)的极限。这个法则可以用来求解一些复杂函数的极限。
5. 泰勒级数展开:对于一些复杂的函数,可以通过泰勒级数展开将其展开成多项式之和的形式。这样可以将复杂的函数转化为简单的多项式,从而简化计算。
6. 等比数列的极限:等比数列的极限可以通过等比数列的定义来求解。设{an}为等比数列,公比为q,首项为a1,则lim an=a1*lim1/q。