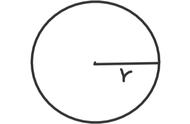
如上图,证明基于以下两个事实。
OA<OB, P(A)Q<弧PBQ
断言四:给定一个已知圆,做圆的内接正多边形,正多边形的边数越多,正多变形的面积更接近圆的面积。如正八边形的面积比正方形更接近圆的面积,正十六边形又比正八边形更接近圆的面积,这一过程可以无限继续,则正多边形的面积无限逼近圆的面积。(跟我国魏晋期间刘徽的割圆术类似,都用到了穷竭法)
显然,圆内接正多边形的面积永远小于圆的面积。但是,如果预先给定任一面积,不论其多小,我们都能做出一个内接正多边形,而使圆面积与其内接正多边形的面积之差小于这一预先给定的面积。(是不是有熟悉的感觉,这恰是高等数学中极限的定义,这也是阿基米德证明圆的面积的关键。)
断言五:任意圆外切正多边形的面积大于圆的面积。

圆外切正多边形
设 δN=SN-S圆>0
SN为圆外切正N边形的面积,δN为圆外切正N边形面积与圆面积之差,即图中阴影部分的面积。
参考断言二易知 δ2N<δN/2
断言六:定义三角形的面积小于圆外切正N边形的面积。(参考断言三)
断言七:圆外切正多边形的面积永远大于圆的面积。但是,如果预先给定任一面积,不论其多小,我们都能做出一个外切正多边形,而使圆面积与其外切正多边形的面积之差小于这一预先给定的面积。
(四).阿基米德采用的逻辑方法——双重归谬法(反证法)
在阿基米德之前,人们往往采用直接证明的方法,而阿基米德则采用间接方法。
比如我们要证明A=B,当直接证明比较困难的时候,可以采用排除法。A与B的关系只有3种情况,A>B,A<B,A=B。如果能排除前两种情况,自然得到A=B。
阿基米德采的方法:排除S圆>S△和S圆<S△两种情况,得S圆=S△。
(五).阿基米德的证明
求证:任意圆的面积,与两条直角边长分别为该圆半径和周长的直角三角形的面积相等,即S圆=S△。
第一步,证圆的面积不大于定义三角形。
证明:
假设 S圆>S△
令 ε'=S圆-S△>0 (预先给定的面积)
根据断言四
当取充分大的n,使得 δn<ε (δn见断言一,根据断言四)
有 Sn<S△<S圆 (断言三)

这表明 ε=S圆-S△<S圆-Sn=δn (如上图)
即 ε<δn
与n的选取矛盾,则假设S圆>S△不成立。
第二步,证定义三角形的面积不大于圆。
证明:
假设 S△>S圆
令 ε’=S△-S圆>0 (预先给定的面积)
根据断言七
当取充分大的N,使得 δN<ε' (δN见断言五,根据断言七)
有 S圆 <S△ < SN (断言六)

这表明 ε'=S△-S圆<SN-S圆=δN (如上图)
即 ε'<δN
与N的选取矛盾,则假设S△>S圆不成立。
综上第一步第二步证明,可知 S△=S圆。
用阿基米德的语言描述为:“由于圆的面积既不大于、也不小于(三角形面积),因此,圆的面积等于三角形面积。”
(六).想到的一些闲话
- 从阿基米德的证明过程可以看出其严谨的思维,奇特的方法。在他的时代,这种反证法是一种绕圈子式的论证,在他之前,圆的面积是包括欧几里得都没能解决的问题,可见其困难和复杂的程度。
- 就像建一座房子,阿基米德每一块石头都需要自己亲手凿,用最原始的方式建了一栋房子,而这房子屹立千年,现在依然完好。
- 遗憾的是,阿基米德的证明最终只是用三角形的面积表示,并没有发现π的存在。但阿基米德随后在《圆的测定》第三个命题中,推导出了π的范围约为3.14。(知道存在这样一个常数,没有把周长中的常数与面积中的常数联系起来。)
- 圆的面积证明只是阿基米德数学遗产的一部分,其其他著作中论述的问题已经属于今天的微积分领域了。
- 由于所处的时代限制,没有简明的代数符号,阿基米德只能依靠陈述,犹如戴着镣铐跳舞。
- 阿基米德是被罗马士兵*死的。
1.刘徽的割圆术