归纳起来,对于有n个节点和b条支路的电路,一定有(n-1)个独立的 KCL 方程,(b-n 1)个独立的 KVL 方程,还有b个独立的 VCR 方程。联立求解这 2b个方程,可得各支路电流和电压。这就是所谓的 2b方程法。
2.1.2 支路电流法以电路中各支路电流为独立求解变量的解题方法称为支路电流法。观察式(2-2)和式(2-3),如果将各支路的 VCR 关系代入式(2-2)中,就可得到以支路电流表示的 KVL 方程,它们再和独立的 KCL 方程联立求解,总共只有b个方程,从而简化了分析。

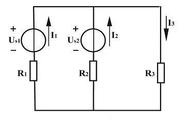
若把流过同一电流的串联元件作为一条支路,在图 2-2 中共有三条支路和两个节点。若选 b 为参考点,则对节点 a 有一个独立的 KCL 方程,即
- i 1 i 2 i 3 =0
选网孔为独立回路,并按 l 1 和 l 2 的巡行方向可列两个独立的 KVL 方程,即
- u S1 R 1 i 1 R 3 i 3 =0
- R 3 i 3 R 2 i 2 u S2 =0

由此可得出支路电流法的一般步骤:
(1)假设各支路电流的参考方向和网孔的巡行方向。
(2)对( n -1)个节点列 KCL 方程,对( b - n 1)个网孔列写以电流变量表示的 KVL 方程。
(3)求解各支路电流,进而求出其他所需量。
2.2 网孔分析法
网孔分析法的步骤如下:
(1)选定一组网孔,并假设各网孔电流的参考方向。
(2)以网孔电流的方向为网孔的巡行方向,按式(2-9)的形式列写各网孔的 KVL 方程。
(3)由网孔方程解出网孔电流。原电路非公共支路的电流就等于网孔电流,公共支路的电流等于网孔电流的代数和。

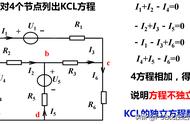
在图 2-3(b)中,除节点 d 外,可列出三个互相独立的 KCL 方程为