需要解释的是,我个人很喜欢数独,很多技巧是在玩的时候慢慢悟的,网上也有看到过一些技巧,但似乎没有什么标准的命名方法,因此我就按照自己的喜好随便取名字了,反正,叫什么不重要,重要的是掌握这种技巧。
三缺一
在数独里,最简单的莫过于就缺一个数了,在四宫格里,体现为三缺一,就是在同一行或者同一列或者同一宫里,1-4已经有了3个,你只需要填写出最后一个即可。
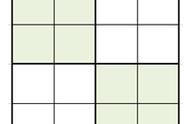
以下图为例,就是最适合小朋友初次尝试的四宫格题目。

我们可以看到,在左上角的宫里,已经出现了1、2、3三个数字,独缺4,所以很容易确定B2格应该是4;
当我们在B2格里填写了4以后,很自然,B行也出现了三缺一,1、3、4独缺2,所以B4格就是2;
同理,A3格就是3,此时第3、4列都出现三缺一的情况,按此规则即可轻松完成这道数独题目。

这种三缺一,推广到九宫格,自然是在一行或列或宫中出现了1-9中的8个数字,独缺的那个数很容易就推算出来了。
非常建议的是给小朋友出一些这种九宫格的题目,因为这需要小朋友观察出到底哪个行或列或宫中出现缺一的情况,而且需要他从1-9一个个数过去才能判断出来到底缺了哪一个。
二缺二
在小朋友轻松掌握三缺一的补缺技巧后,作为循序渐进的第二步,我们就可以把题目扩展到二缺二了,就是1-4里只有2个,需要你补上剩余的2个,通常,需要用到交叉排除法。
所谓交叉排除法,就是当一个格子里可能出现几个不同的数字,但是这一个格子所在的行或列或宫中,已经有了其中一个数字,那么这个格子里就不可能再出现这个数,举例:

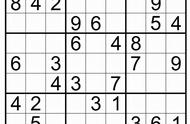
上图中,我们先看右上角的宫,其中有了1、4,所以在A3格和B4格中只能是2或者3;
但是我们注意到第4列中已经出现了数字3,在C4的位置,所以B4格原本可能是2和3,现在3被排除了,只能是2了;
很显然,通过三缺一,我们继续确定了A3格是3,D4格是1,C3格是2;
此时,又出现多个二缺二的情况,经过观察,A行剩余的A1、A2格可能是1或者2,由于C2已经是1了,所以A2就只能是2,A1自然是2了;
继续按规则走下去,也很容易完成这个题目。

个人建议
1.我们已经看到,即便是四宫格,我去掉的数字比较多,导致这个题目完成起来难度也不小,可以考虑多增加几个数字,降低难度,以后逐步增加难度;
2.这个技巧非常非常考验观察力和逻辑分析能力,尤其扩展到九宫格以后,小朋友可能不太适应,但练习一段时间后,他在观察力和逻辑分析方面的提升,会很明显,强烈建议多练习这样的题目,不要着急上后面的。只有这方面基础打好了,才能继续下一步学习新技巧;
3.虽然也有一些辅助教具用来做数独,甚至也有APP做,但我个人更建议自己出题,打印在纸上,更有利于提升他的观察能力。
等我空了,我也针对这些技巧一些题目,放到excel里,供需要的下载打印。
有兴趣的也可以看我同名的wx公众号(heima_yuer)
,