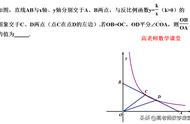
前边讨论了,知道物体的运动方程,可以用导数计算它的速度方程。
现在考虑逆问题,知道了一个物体的速度方程,那它的运动方程是什么样的?

双向车道车在相反方向行驶
比如知道了 一个物体 速度随时间的 变化为 gt,那它的运动轨迹是什么样子的。
从计算的角度看,就是找一个方程,使它的导函数等于速度方程。
假设用一个运动方程求导数得到一个速度方程,现在的问题是,通过求导数能得到这个速度方程的 运动方程 是唯一的吗?
不是唯一的,但是这些多个运动方程之间的 差值都是常数项。
速度方程 是 体现距离随时间的变化率的,它里边没有包含物体初始的位置信息,所以多个运动方程 ,虽然对应的速度方程是相同的,但是它们的初始位置可以不同,体现在运动方程上,就是差一个常数项。
虽然运动方程有多个,它们都对应同一个速度方程,但是只要确定了起始时间和结束时间,物体在这段时间内的经过的距离,位移就是相同的。

定积分应用例子
从数学上来说,一个速度方程,对应的运动方程,就是这个速度方程 的不定积分,可以把运动方程叫做 速度方程 的原函数。是求导函数的逆运算。
而已经知道一个速度方程,给定开始时间点和结束时间点,这段时间间隔经过的位移,就是求速度方程的定积分。可以用速度方程的任意一个原函数,代入时间上下限,计算出差值,就可以计算出速度方程的定积分了。
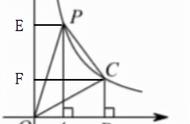
自由落体运动从物体被放开的时间点,到落地前的某个时间点,速度和位移的关系也可以用上边这个图形来表示。

自由落体对应几何图
这个图里,横坐标表示时间,斜线表示速度,面积表示经过的位移。直角三角形底边为t,高为gt,面积为 g 乘以t 的平方的 1/2。
通过这样的图,可以看出,计算定积分不止可以通过速度方程计算出物体在固定时间间隔内的距离,其实计算的也是速度方程曲线x 轴围成的面积。
在学习微积分以前,数学课程里有好多图像的面积计算公式,比如长方形,梯形,三角形,圆,扇形。这些图形的面积计算公式,都是通过割补法推算出来的,比如两个直角三角形可以拼接成一个长方形,两个梯形也可以拼接为一个长方形。扇形和圆的面积按中心角成比例。

梯形面积计算公式
但是有些图形是不好通过割补法拼接成已知面积计算公式的图形的。比一个抛物线和x 轴围成的面积。椭圆的面积。指数函数和x轴围成的面积。
有了微积分,就可以通过计算这些函数在自变量的一个区间上是定积分,来轻松算出这些图形的面积。
这样,微积分化割补法技巧为积分运算,
化不可能为可能。
化复杂为简单。
微积分是如何做到这一点的,
它和割补法思维的本质差别在哪里?
关键是微积分是 通过对运动现象的研究发展出来的。它自身里边就包含了运动思维。把事情的变化率作为考虑事物的出发点。

风车通过风的运动提供动力
这样把图形的面积理解为图像随x轴延伸,函数图像曲线和x 轴 围成区域的变化量。
而割补法只是把几个固定的图像凭借在一起。虽然有一定的运动,但是只能考虑到少数运动。
微积分的这种通过运动,通过变化率来理解事物的思维方式,革新了人们对许多数学问题的理解,把数学的力量推到了前所未有的新高度。
,